 |
|
|
[Sponsors] | |||||
Fully coupled solver (incompressible N.-S.) - Determinig pressure up to a constant |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
I implemented a fully coupled solver for the incompressible Navier-Stokes Equations (solves for u,v,w,p simultaneously) according to Darwish:
http://www.sciencedirect.com/science...21999108004725. I want to verify my program using a manufactured solution. For this I am applying dirichlet boundary conditions for the velocities to ALL of my boundaries. According to Darwish's paper I have to extrapolate pressure at those boundaries (Neumann BC). Analysis of the resulting system shows, that my system is not singular. Furthermore depending on the way I chose the preconditioner settings I get different results for the pressure. Note that I cannot apply a direct solver without generating zero pivots due to the bad condition of the linear system. However I observe that two results for pressure coming from different preconditioner settings only differ by a constant. The results for the velocities remain indifferent to those settings. On the other side, using a segregated approach (SIMPLE), the system for the pressure correction is, due to the use of Neumann BCs, always singular (nullspace of the respective matrix has dimension 1). So the homogeneous solution of this linear system, the vector that spans the nullspace (constant vector, i.e. all entries have the same value), can be added to the special solution an hence shift the pressure level. Shouldn't the system resulting from the fully coupled FVM discretization be singular, too (nullspace of dimension 1), so the pressure would exhibit the same behaviour? |
|
|
|

|
|
|
|
|
#2 |
|
New Member
kiyoung kim
Join Date: Oct 2014
Posts: 5
Rep Power: 11  |
I am not fully understand your question but constant difference in pressure difference do not affect your solution. You only need pressure difference in Navier Stokes equation. absolute preesure value varies depending on solver or boundary condition.
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
Let me amplify the question for the sake of clarity:
Why is the system that I get from a fully coupled discretization nonsingular whereas the system for the pressure correction that I get from a segregated approach is singular? I think the coupling of the rows for (u,v,w) and (p) in the linear system takes care of the singularity but this is just a guess, not a proof. I don't need boundary conditions to change the pressure level up to a constant in the segregated approach, the singularity of the system matrix for the pressure correction already allows me to add a vector of the associated nullspace to my pressure correction and change the pressure level accordingly. Why don't I have this opportunity in the coupled approach? Last edited by eltenedor; November 11, 2014 at 15:32. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
If I am right, you are wondering why the global matrix in the system (see attache image) is not singular while the pressure matrix is singular?
|
|
|
|

|
|
|
|
|
#5 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
This is correct. The global system for
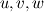 and and 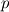 in its most general form for in its most general form for 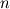 control volumes looks like this (no field interlacing): control volumes looks like this (no field interlacing): where  . .If I compare Matrix coefficients I can prove that the Matrix 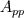 is the same one I use for the pressure correction equation in the segregated approach (SIMPLE algorithm). I exported the matrix for a two dimensional test case ( is the same one I use for the pressure correction equation in the segregated approach (SIMPLE algorithm). I exported the matrix for a two dimensional test case (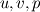 ) to matlab and extracted the matrix block corresponding to ) to matlab and extracted the matrix block corresponding to 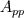 . This matrix block has the vector . This matrix block has the vector 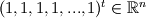 spanning the nullspace of spanning the nullspace of 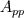 just as in the segregated approach. just as in the segregated approach.For completeness I will attach an example matrix in ASCII format so anyone interested can analyse it with the means of their choosing. Note that I use field interlacing - speaking in terms of Matlab: Code:
A_pp = A(i,i) Code:
i = 3:3:size(A,1) |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Ok, note that the bc.s are relevant for the matrix structure
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Segregated, projection metods, etc can be seen in terms of approximate factorization of the original matrix. Some papers of Perot explained that
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
Note that I apply Dirichlet boundary conditions for velocity on every boundary and Neumann boundary conditions for pressure on every boundary. Is this allowed for a coupled solver? I used this set of BCs to verify a segregated solver (SIMPLE algorithm) some time ago and it worked flawlessly.
Does this further Information help you in understanding singularity / nonsingularity of my system matrix, i.e. does my system matrix behave as expected from the BCs I apply? |
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Quote:
|
||
|
|

|
||
|
|
|
#10 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
Yes, this is the expected behaviour for the pressure / pressure correction equation. I think this reflects the property of incompressible flows that says that pressure can be determined only up to a constant. However by coupling this equation with the velocities former singularity gets lost. Do you have an explanation for this?
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Several references are reported here
http://www.maths.manchester.ac.uk/~d...unsteadyNS.pdf |
|
|
|

|
|
|
|
|
#12 | ||
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
Quote:
Quote:
|
|||
|
|

|
|||
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
||
|
|

|
|
 |
| Tags |
| coupled solver, finite volume method, incompressible flow, pressure based solver, singularity |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How to read pressure at discrete points | paka | OpenFOAM | 16 | April 28, 2020 07:26 |
| Pressure force calculation in incompressible solvers | philippose | OpenFOAM Running, Solving & CFD | 10 | December 7, 2019 04:51 |
| Some confusion about coupled solver for incompressible flow | bearcat | Main CFD Forum | 0 | February 14, 2010 20:40 |
| flow simulation across a small fan | jane luo | Main CFD Forum | 15 | April 12, 2004 17:49 |
| what the result is negatif pressure at inlet | chong chee nan | FLUENT | 0 | December 29, 2001 05:13 |