| liljendal |
June 4, 2015 04:32 |
Anderson's "Numerical solutions of quasi-one-dimensional nozzle flows"
Hi,
I am currently reading through chapter 7 "Numerical solutions of
quasi-one-dimensional nozzle flows" of the book "Computational Fluid
Dynamics, the basics with applications" by John D. Anderson - and got
stucked at the following step:
Let us obtain from Eq. (7.33) the nonconservation form expressed in
terms of internal energy by itself. The latter can be achieved by
multiplying Eq. (7.23)
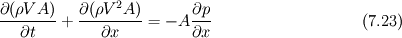
by V, obtaining
![\hspace*{3cm}
\frac{\partial [\rho (V^2/2)A]}{\partial t}
+ \frac{\partial [\rho (V^3/2)A]}{\partial x}
= - AV \frac{\partial p}{\partial x}
\hspace*{2cm}(7.34) \hspace*{3cm}
\frac{\partial [\rho (V^2/2)A]}{\partial t}
+ \frac{\partial [\rho (V^3/2)A]}{\partial x}
= - AV \frac{\partial p}{\partial x}
\hspace*{2cm}(7.34)](/Forums/vbLatex/img/c68b80f70fc84a3c08f77147d373fe81-1.gif)
Could somebody please explain why Eq. (7.23) multiplied with V results
in Eq. (7.34)?
Thanks a lot,
Leo |


![\hspace*{3cm}
\frac{\partial [\rho (V^2/2)A]}{\partial t}
+ \frac{\partial [\rho (V^3/3)A]}{\partial x}
= - AV \frac{\partial p}{\partial x} \hspace*{3cm}
\frac{\partial [\rho (V^2/2)A]}{\partial t}
+ \frac{\partial [\rho (V^3/3)A]}{\partial x}
= - AV \frac{\partial p}{\partial x}](/Forums/vbLatex/img/48b906b34036f1babc5d96cb53c1cf83-1.gif)
![\hspace*{3cm}
\frac{2V}{2} \frac{\partial [\rho V A]}{\partial t}
+ \hspace*{3cm}
\frac{2V}{2} \frac{\partial [\rho V A]}{\partial t}
+](/Forums/vbLatex/img/0674dfa3e0b4edcfbc6f7b1aff411f57-1.gif)
![\frac{3V}{3} \frac{\partial [\rho V^2 A]}{\partial x}
= - AV \frac{\partial p}{\partial x} \frac{3V}{3} \frac{\partial [\rho V^2 A]}{\partial x}
= - AV \frac{\partial p}{\partial x}](/Forums/vbLatex/img/db43044b62b50c982f510f3833688776-1.gif)
![\hspace*{3cm}
V \frac{\partial [\rho V A]}{\partial t}
+ \hspace*{3cm}
V \frac{\partial [\rho V A]}{\partial t}
+](/Forums/vbLatex/img/770349ce5b0e829c191ebe8ae2d31818-1.gif)
![V \frac{\partial [\rho V^2 A]}{\partial x}
= - AV \frac{\partial p}{\partial x} V \frac{\partial [\rho V^2 A]}{\partial x}
= - AV \frac{\partial p}{\partial x}](/Forums/vbLatex/img/7c3b03aa5365958f0876fa7557bd289f-1.gif)