Diffusion Equations coupled by Boundary Conditions
 

Hi, I'm new here and not sure whether my question is in the right place.

I have the following problem:

I'd like to solve two diffusion equations, e.g.

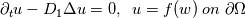
and


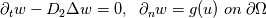
which means the PDEs are coupled by their boundary conditions.
The solution of u depends on w by a Dirichlet BC.
And w depends on u by a Neumann BC.

At the moment I first solve the equation for u, then compute g(u) and afterwards solve the equation for w, which allows me to compute f(w) for the next iteration, etc. ....

This works very nice for the stationary case, i.e. for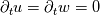
For the time dependent case however....the method is highly unstable.

I'm searching now for a method to solve both equations simultaneously, somehow - instead of one after another.

But I have no clue how to do this. If one searches for literature about this issue, it seems nobody has ever had the problem to solve PDEs coupled by boundary conditions.

Any hint? Any literature? Ideas?

BTW: I'm not working with any commercial software, but a own FEM software written in Fortran. Therefore please don't recommend commercial software.

Greetings,
Amiga-Freak

numerical instability appears if you do not use a time step within the stability region. What criterion have you used?

Well, there you have me....
I have not given much thought of this at all, so far :o

What about the functions for the bc.s ?

What do you like to know about them?

It seems that your instability (I am saying this without knowing anything about the way you implement this numerically...) is due to the fact that while the equation system is elliptical (everything happens instantaneously everywhere at each time-step), you introduce a time-lag between the first equation and the second.

Did you write the solver yourself?
In that case, writing it to solve the two equations at the same time should be straight-forward. A more elegant solution would be to write the solver as implicit. Compared to Navier-Stokes equation, your set is relatively simple and, above all, linear. This means that the implicit solver, even in 2D and 3D, remains quite simple.
The advantage is that the boundary conditions are imposed at the same of the solution.

If you did not write the code, you may "trick" the solver into solving both equations (they are the same) by using a vector that is twice as big {u | w} instead of each vector {u} and {w}

The set of equations is parabolic in the unsteady case and classical numerical integrations, such as the Crank-Nicolson method, can be used.

The only care is to provide BC.s that ensure that the time derivatives do not blow-up. For example, the Neumann BC.s for w can be critical, it is simple to see that by integration over the whole computational domain V:

d/dt Int [V] w dV = D2 Int[S] g(u) dS


Therefore, if g(u) is such that Int[S] g(u) dS > 0 then the integral of the w will blow-up in time

Thanks for the correction, FMDenaro. I guess I overlooked the derivative over time.
I agree, parabolic --> Crank-Nicholson

Please, disregard my previous comment

No, I'm a PhD student and the solver was written by other PhD students before me, several years ago.

That was actually the first idea, I had. But my problem is that I don't know how to impose the boundary conditions - because they are dependent on the solutions u and w.
Maybe It's easy and I'm just dumb, but I don't see how to do this.