 |
|
|
[Sponsors] | |||||
Boundary Conditions at Corners, lid driven cavity |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 204
Rep Power: 16  |
I am experiencing some difficulties capturing the secondary vortices for the lid driven cavity and I suspect it has to do with the boundary conditions. I am using the Artificial Compressibility method with 4th order Runge-Kutta in time, 3rd order spatial reconstruction (FV) and 4th order for the diffusive fluxes. My mesh is 128*128 cells and Re=100.
I have been testing the solver now quite a bit and it seems to work just fine for the channel (well, no surprise really) but the lid driven cavity is giving me a hard time. I searched this forum but nothing on my specific problem and I have been going through the literature (Sani and Gresho mainly) but no luck there either. For the boundary conditions, I am using Dirichlet for velocity everywhere and Neumann for pressure (i.e. dp/dn=0, neglecting diffusive fluxes). This seems to work fine for other cases tested, also those containing corners (backward facing step, sudden expansion) and i get correct reattachment lengths but for the lid driven cavity my corners seem to introduce non-physical effects, prohibiting the capturing of the secondary vortices (attached a picture of the u-velocity contours with streamlines). Is there any special treatment/care we have to apply at corners and/or is there anything else that I am missing for the lid driven cavity in terms of boundaries? (it might not just be a pressure boundary issue). just as a note, for imposing boundaries i use ghostcells in my solver, so the exact boundary conditions are met at the boundaries themselves, but since it is finite volume and i store everything at the cell center (collocated approach), the cell nearest to solid boundaries does not have zero velocity components. 
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,763
Rep Power: 71    |
Some comments:
1) As you are using the u,v,p formulation, the streamline functions you posted are not directly used in the solver. Therefore, check if this post-processing is well done, I see streamlines going in and from walls. Generally, the check of a solution must be done on the solved variables, so check the velocity profiles compared to those reported in Ghia & Ghia 2) Check the divergence-free constraint, are the values quite low? 3) Give more details about your FV discretization. How did you discretize the flux integrals? I would see how the corners values enter into the flux computation. The faces adjacent the walls give simly the condition that the convective flux vanishes, without any ghost points. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 204
Rep Power: 16  |
answers, in order
1) good point, will implement the stream function and solve for psi to check, however, in previous solvers i used/programmed, there was never a problem with displaying the streamlines (and i didn't want to blame someone elses software first before not trying to find the error in my code). i checked with tecplot now as well, same result. for the channel flow (and interestingly for the sudden expansion) i have now "seemingly" issues with displaying the streamlines, reattachment is predicted well, which adds to my confusion. i checked also with ghia et al., here is the plot for both u and v velocity along the centerline, not too bad.  2) i check my residuals for u, v, p and the diveregence which is the slowest to converge (as i would expect). in this case the tolerance was 10^(-4), but since divergence took some more iterations to converge, u,v and p were around 10^(-5). 3) if we just look at 1D, the domain looks like that (and then of course for the y(j) direction)  i use the following third order approximations (from Shapiro, E. and Drikakis, D., "Artificial compressibility, characteristics-based schemes for variable density, incompressible, multi-species flows. Part I. Derivation of different formulations and constant density limit", Journal of Computational Physics, Vol. 210(2), pp.584-607, 2005.) 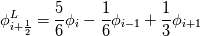 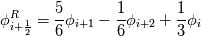 where I use backward (i.e. the left values) for approximating velocities (in the continuity and momentum equation) and forward (right values) for the pressure. I should also say that it seems to be a problem independent of the order of approximation, for higher order (up to 11th order WENO) I still have the same issues, so thats why i suspect the boundaries to be the issue. The stencil requires 2 ghostpoints on the boundary which i then fill with Dirichlet: 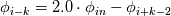 Neumann: 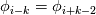 where [math]\phi_{in}[\math] is the specified Dirichlet condition and k=1,2 in this case. So specifically for this case, North wall: u = Dirichlet( 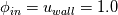 ), moving wall ), moving wallv = Dirichlet(  ), no-slip wall ), no-slip wallp = Neumann All other walls: u = Dirichlet(  ), no-slip wall ), no-slip wallv = Dirichlet(  ), no-slip wall ), no-slip wallp = Neumann with this approach, each ghostpoint is uniquely defined but i am still wondering if there is anything wrong with this approach |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,763
Rep Power: 71    |
ok, apart from the fact that you do not need ghost points (just set to zero the convective flux on the face and use asymmetric first derivative for the normal derivative), the velocity profiles appear correct, therefore I suspect that the problem is only in implementing the post-processing with the streamline.
Decrease the threshold for the divergence and check the residuals to ensure a correct steady state. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 204
Rep Power: 16  |
i am aware that i don't need ghostcells but the solver is now based on that and i feel a bit reluctant to change the data structure (not for laziness reasons, i want to have my higher order schemes uniformly across the domain, i.e. WENO everywhere, also at the boundaries, actually, especially at the boundaries)
yesterday i had the idea that because the solution saved at the cell centers, the velocity won't be zero at the boundaries, so maybe that would solve it (i.e. post processing error), now i changed that and store the velocities at the vertices so that there is zero at the boundaries but the problems still exists. i ran another simulation where divergence has converged now to 10e-14 but still the same, i.e. i still suspsect something strange to b going on with the boudnaries. in general, is there any special treatment for corner points? i am probably haunted by my lattice boltzmann past where corners and edges all present their very own unique challange ... |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,763
Rep Power: 71    |
But what is more accurate than setting the exact vanishing convective flux at wall?
The two upper corners have singular values, to treat them you have to regularize by extracting the limits. But I worked on the lid driven cavity more than 20 years ago up to high Re number (10000), I had no problem with high accuracy due to the corner values. Again, from the computed solution the velocity profiles appear correct, therefore I would check the postprocessing you are doing for the streamlines. Are you solving Lap Psi = curl v ? |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 204
Rep Power: 16  |
not yet but will give that a go and see what i get from it. thanks for your input
|
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,763
Rep Power: 71    |
Quote:
good, I am quite sure that the streamlines you plotted do not correspond to the resolved velocity field, at least looking to the velocity profiles at the centerlines.... however, let me know also if you try setting directly flux_convective(i-1/2,j)=0. |
||
|
|

|
||
|
|
|
#9 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 204
Rep Power: 16  |
just wanted to "close" this thread, in case someone stumbles upon this thread (most likely myself in the future, wouldn't be the first time
 ... ) ... )it was the fluxes at the boundaries, they were not exactly zero (at wall boundaries). I set them now to zero and don't need one-sided approximation. what i forgot to do initially was to balance the diffusive fluxes, so the diffusion term was actually responsible for wall velocities (and strange wall velocities, accumulated over time). so now i set my boundary conditions (ghost cells) before entering the time/space loop and first compute the diffusive fluxes (velocity at wall will still be zero) and then i compute the inviscid fluxes (non-linear term) and set them to zero at walls, this way it is working nicely). Thanks again for the help! |
|
|
|

|
|
 |
| Thread Tools | Search this Thread |
| Display Modes | |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Centrifugal fan | j0hnny | CFX | 13 | October 1, 2019 13:55 |
| CGNS Boundary conditions using SU2 | denzell | SU2 | 3 | July 9, 2018 05:58 |
| Radiation interface | hinca | CFX | 15 | January 26, 2014 17:11 |
| Low Mixing time Problem | Mavier | CFX | 5 | April 29, 2013 00:00 |
| Water subcooled boiling | Attesz | CFX | 7 | January 5, 2013 03:32 |