 |
|
|
[Sponsors] | |||||
Numerical treatment of the source term in combustion equations |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear all,
I have a question about how to treat the chemical source term within a PDE correctly. I am trying to solve the flamelet equations, given as: 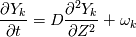 a) Time term is simple (I am using a Euler scheme for that) b) Diffusion term is simple (I am using a center differencing scheme for non-uniform spacing) Source Term Treatment I am not sure if I can calculate the species mass fraction segregated because these terms are coupled. I do not know how to treat the source term. For example: a) Can I calculate the source term omega for each species before calculating the species equation. b) Do I have to use some other method (I read about Jacobian Matrix) c) Explicit or Implicit treatment Finally, I could not find any literature where it will be probably described how we would treat this term. Any suggestions are welcomed. Thanks in advance, Tobi
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I am interested in reading other's replies and any references. I had to implement similar source terms when modeling fuel cells a long time ago. Let me give you my experiences and you can take them for what they are worth.
The classic source term linearization approach is not helpful here. The first reason is the multiple dependent variables. If you are solving the species transport equations in a segregated manner, the dependence on the solved variable is going to be largely ineffective in capturing source terms changes. Building the full Jacobian for the source term and solving the system as a coupled linear system may avoid this problem, but that raises another issue. The normal rationale is to linearize the source term and to deposit the linearized term only the diagonal of the matrix (whether segregated or coupled) only if it makes the matrix more diagonally dominate. Otherwise, it is not linearized and just added to the right-hand side. So, depending on the sign of the linearized factor, the source terms will be treated differently. That is a big problem for chemical species conservation. If you have a null species (like N2) in your system that is calculated as Y_N2 = 1 - sum_k (Y_k), you will see N2 produces or destroyed as your system converges and evolves. That is because the source terms need to stay balanced to machine precision for the chemistry fields to remain consistent. Failure to maintain this (say, keeping species fraction summing to 1 within some converged tolerance) will not work in my experience. The results will be worthless. That led me to not linearize any of the source terms and to apply them exactly as calculated and added them to the RHS of the segregated solver. I also verified that the sources all balanced perfectly in each cell (mass of O2 and H2 disappearing exactly matched the mass of H2O appearing, say). This led to convergence that was slower than I would have liked, but it worked. If you under-relax your species equation solution, I'd caution you to use the same factor for all of the species equations too, again for consistency sake. Good luck. |
|
|
|

|
|
|
|
|
#3 | ||||
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Prinkey,
first of all thank you for the replay. I was also discussing about that topic with my colleague yesterday (he is also very familiar with the discretization but not with that kind of sources). In any case, you gave new and good input. Let me be summing up your answer, if I got it correct. Quote:
![Y_{k,i}^{new} = \left[\frac{\chi}{2}\frac{Y_{k,i-1}^\mathrm{new} - 2Y_{k,i}^\mathrm{new} + Y_{k,i+1}^\mathrm{new}}{\Delta Z^2} + \underbrace{\omega_{k,i}^\mathrm{old} + \sum_{s=1}^n{\left.\frac{\partial [X]_k^\mathrm{old}}{\partial Y_s}\right|_i} \left(Y_{s,i}^\mathrm{new}-Y_{s,i}^\mathrm{old}\right)}_{\mathrm{linearization~of~}\omega_{k,i}^{new} }\right] \Delta t + Y_{k,i}^{old} Y_{k,i}^{new} = \left[\frac{\chi}{2}\frac{Y_{k,i-1}^\mathrm{new} - 2Y_{k,i}^\mathrm{new} + Y_{k,i+1}^\mathrm{new}}{\Delta Z^2} + \underbrace{\omega_{k,i}^\mathrm{old} + \sum_{s=1}^n{\left.\frac{\partial [X]_k^\mathrm{old}}{\partial Y_s}\right|_i} \left(Y_{s,i}^\mathrm{new}-Y_{s,i}^\mathrm{old}\right)}_{\mathrm{linearization~of~}\omega_{k,i}^{new} }\right] \Delta t + Y_{k,i}^{old}](/Forums/vbLatex/img/88b0e5f5bd894336aa17ec43aa4f9b98-1.gif) Here the derivative is the Jacobian matrix (its clear). You told, that this will start another problem. Which one? Quote:
Quote:
Quote:
Summing up I should solve the linear system as (laplacian term can be treated implicit or explicit): ![Y_{k,i}^{new} = \left[\frac{\chi}{2}\frac{Y_{k,i-1}^\mathrm{new} - 2Y_{k,i}^\mathrm{new} + Y_{k,i+1}^\mathrm{new}}{\Delta Z^2} + \omega_{k,i}^\mathrm{old}\right] \Delta t + Y_{k,i}^{old} Y_{k,i}^{new} = \left[\frac{\chi}{2}\frac{Y_{k,i-1}^\mathrm{new} - 2Y_{k,i}^\mathrm{new} + Y_{k,i+1}^\mathrm{new}}{\Delta Z^2} + \omega_{k,i}^\mathrm{old}\right] \Delta t + Y_{k,i}^{old}](/Forums/vbLatex/img/ab9328b96ddccff60e72784adcdab607-1.gif) I just have a question about the time step 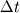 that I am calculating based on the Fourier, the diffusion term that I am calculating based on the Fourier, the diffusion term 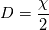 and the minimum mesh spacing. If I would have a scalar dissipation rate of 1e-8, and the minimum mesh spacing. If I would have a scalar dissipation rate of 1e-8, 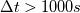 . I am sure that this can make trouble or not? Is there another time step criterion based on the chemical reactions? Based on the flamelet theory, the calculation domain is a 1D domain and based on the equation (without source term), the stability criterion for explicit treatment would be that the Fourier number is smaller than 0.5. However, I have the feeling that this is not the correct way for estimating the time step, isn't it? . I am sure that this can make trouble or not? Is there another time step criterion based on the chemical reactions? Based on the flamelet theory, the calculation domain is a 1D domain and based on the equation (without source term), the stability criterion for explicit treatment would be that the Fourier number is smaller than 0.5. However, I have the feeling that this is not the correct way for estimating the time step, isn't it?Thanks in advance for any further suggestion and other replays.
__________________
Keep foaming, Tobias Holzmann |
|||||
|
|

|
|||||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Have you a stiff source term? What about the time scales of the action of the several terms?
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Yes, I think you understood me. The second problem was what I mentioned in the next paragraph...conservation of species with differing linearizations. The construction of the Jacobian can be done and it can be used to linearize source terms for a fully coupled species/energy linear system. And that linearization can be made consistent, but ONLY if all of the linearized terms are treated the same way...either all added to the diagonal or all dumped to the RHS. Doing the latter is equivalent to not linearizing at all. Doing the former will potentially ruin diagonal dominance of the matrix which is make it difficult to solve using AMG or preconditioners that that rely on Gauss-Siedel or its variants as smoothers. Maybe ILU smoothers can be made to work, but just know that once you give up diagonal dominance, a lot of things that you casually assumed will work, may not anymore.
The easiest way to code this is the one I recommend--explicitly compute source terms using old iteration values and apply them without linearization. If you are doing steady solutions, your algorithm as listed should be fine. If you are doing transient computations, you will likely need to do some non-linear subcycles to converge each timestep. And you will almost certainly need under-relaxation. Or you will have to take very (very) small timesteps. I should also mention two other things. First, the energy equation needs to be treated exactly the same way...explicit source terms and the same under-relaxation factor as used for the species. I alluded to this above. This is for exactly the same reason--inconsistencies in the species compositions and related formation enthalpies will make the temperatures and reaction rate calculations inconsistent and you will get nonsense. The second thing is that you may wish to consider the use of fractional time-stepping for the reaction portion of the system. This is the way so-called stiff chemistry solvers are applied. It avoids the source term issue entirely and simply treats each finite volume as a fixed mass reactor and integrates each to the new timestep separately, often using a stiff ODE solver. The results then overwrite the old time values. Then the normal transport part of the system is solved to account for spatial terms. This is often essential to getting good performance from systems that have fast chemistry...say at a flame front. There, the characteristic time may be many orders of magnitude shorter than that of the bulk transport or of the chemistry in cooler cells. So, using a cell-by-cell ODE solver allows very small timesteps to be taken adaptively to move forward in time without forcing those the small timestep limit on all of the cells and all of the transport terms. Reacting flow is a wholly different beast than cold flow. The extreme changes in temperatures from reactions and the exponential temperature dependence for reaction rates make these extreme measure necessary. I do need to say that I have not implemented the fractional step stiff solver myself, but the principles are well documented. And, again, I have approached this topic only a decade or more ago and not with an eye to comprehensively understand the topic, but just to make something work. Others have likely conceived better approaches to this problem and I am simply unaware. But I do know this to be a tricky problem, so I'm happy to cast what light I can. Good luck. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
Maybe it's just me misunderstanding (in this case, sorry) but, do you refer to the flamelet library pre-computation or to the actual resolution of the flamelet equation?
If, as i got it, it is the first one, i've heard that Cantera has been used for this. As it is open source, you may want to give a look at it: http://www.cantera.org/docs/sphinx/html/index.html Some other information i just got from google which might be relevant: https://openfoamwiki.net/index.php/E...n/flameletFoam http://download2.nust.na/pub4/source...-July-2004.pdf Edit: I have not extensively used it by myself (so i can't point to specific paragraphs), but you might want to give a look at: Oran, Boris: Numerical Simulation of Reactive Flow, Cambridge Last edited by sbaffini; September 6, 2016 at 11:37. Reason: added reference |
|
|
|

|
|
|
|
|
#7 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Paolo,
thanks for your replay. To your questions. You are right, I want to solve the flamelet equations not the normal transport equations for the mixture fraction and its varianz within the cfd solver. The background here is as follow. I am working with OpenFOAM now over 6 years and during my master thesis I was investigating into the libOpenSMOKE toolbox. This is a flamelet-solver for OpenFOAM with a flamelet-calculator as binary version (bad). Two years later, Hagen Müller from Munic published his own flamelet code. There are advantages of both. LibOpenSMOKE has entalpy defects included where as the flameletModel from Müller can be used for LES. Well libOpenSMOKE too but it is not implemented till now. I prefer the lib opensmoke toolbox than the flameletFoam stuff because it is a standalone lib. Due to the fact that I wanted to improve my c++ knowledge I started to develop an own OpenFOAM solver, that includes all advantages of libOpenSMOKE and flameletFoam. The only problem is that the flamelet generation was different for each toolbox.
- How to treat the source term - How to solve the linear system of equations (segregated or coupled) - Implicit or explicit That 's why I was asking,..
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Depending on the required time accuracy, a Strang splitting operator can be adopted.
For example, you can read this paper that (apart from the fact you have diffusion instead of convection) illustrates that: http://ntrs.nasa.gov/archive/nasa/ca...9880008959.pdf You could find help also in this book https://books.google.it/books?hl=it&...oinsot&f=false |
|
|
|

|
|
|
|
|
#9 | ||||||
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Michael,
thanks again for your excellent replay. Quote:
Quote:
Quote:
Quote:
Quote:
Quote:
Summarize Due to the fact that I am interested in the steady-state solution, I could use the last equation in my previous post. The only problematic term is the source term, that is treated explicit. Before I solve the species equation, I will solve this term by using some special algorithm and based on the source terms, I will update the old mass fractions, which are used then to evaluate the new one. Edit. added a PDF
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; September 6, 2016 at 15:19. Reason: BDE -> BDF = Backward differenziation formular + PDF |
|||||||
|
|

|
|||||||
|
|
|
#10 |
|
Senior Member
|
Dear Tobias,
now i am more confident about what we are talking about. You probably know more than me but, have you given a look at these: http://www.sciencedirect.com/science...98135498002336 http://super.chem.polimi.it/download...ent-structure/ http://super.chem.polimi.it/download/bzzmath-download/ https://www.researchgate.net/publica...tic_mechanisms Edit: The whole point of asking about the specific task (flamelet pre-computation vs. general transport equation) was that, probably, as this is a one-shot pre-computation task you may want to develop a separate set of strategies to solve it in the most efficient way (with respect to those in the finite volume solver). As others have said, my feeling is that splitting is the most obvious choice here (also from the software engineering perspective). |
|
|
|

|
|
|
|
|
#11 | |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Paolo,
thanks for the hints and literature Quote:
 Interesting, because they are at the same university than the CRECK modeling (you too Interesting, because they are at the same university than the CRECK modeling (you too  ?). Maybe they used it in the flamelet-creator that come with the libOpenSMOKE tool, too. The last days I realized, after discussions, that the chemical systems (stiff) should be solved with BDF (as implemented and shown in the paper above). I will try to understand the solution procedure and implement it (I am always interested in how to program it)... but the source code can give me further hints. ?). Maybe they used it in the flamelet-creator that come with the libOpenSMOKE tool, too. The last days I realized, after discussions, that the chemical systems (stiff) should be solved with BDF (as implemented and shown in the paper above). I will try to understand the solution procedure and implement it (I am always interested in how to program it)... but the source code can give me further hints.Terrible ... there it is ... I was looking for that stuff for 3 years and the authors of libOpenSMOKE only rarely replayed. So my work is more or less worthless now  ... ... Thanks for the good literature.
__________________
Keep foaming, Tobias Holzmann |
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
|
Well, glad to know that i could manage to help you.
I got my Ph.D. from POLIMI and, while we never actually worked together, i met a couple of times with both Prof. Faravelli and Prof. Cuoci for tasks related with my Ph.D. I can't recall now on what exactly, but they indeed helped me a lot on certain issues. So i guess that the whole point on the library might be due to: the fact that it is not only a work of their own (maybe third party license issues and similar stuff they were not able to manage at that time); as it is a relatively large piece of code (82k lines for just chemics), maybe not everyone in the project knows about everything and collecting the information you were asking could have been more difficult than we imagine. |
|
|
|

|
|
|
|
|
#13 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi,
well 86.000 code lines for the chemistry is much. Mine has now 18.000 but there is nothing included about the solving algorithm and there are still some parts missing. In any case I will try to get it work and publish it too, why not - the work is already done and the main goal was to understand more about programming and numerics. I think the Prof. you mentioned are very good in that what they are doing and - yes - I think the chemistry calculation is a very huge topic. After I started to decide to make a project where I can calculate flamelets, I thought it is not as difficult as I know now. Solving normal (non-reacting) equations are not a big deal but the source term is tricky and even all the calculations that you need to do to get the source terms are not straight forward. I also had to dig into gas kinetics  - so finally I learned really a lot. - so finally I learned really a lot. By the way, I realized last year, that CRECK modeling did not offer the libOpenSMOKE library anymore and they switched to the laminarSmoke. I never tried the solver but I read some PDF that it is for laminar flow and not turbulent anymore. Well, they did a great job and I am happy that I could use their model in my master thesis. Thanks again. I will try to calculate the source term using BDF's and hope to get a good solution. By the way, does anyone know how to estimate the timestep for the chemistry calculation?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,273
Rep Power: 34   |
||
|
|

|
|
|
|
|
#15 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Arjun,
thanks for the hint but I do not have the book at the moment. I will check if it is in the public library  Tthere is just one question left for now. Which BDF could or should be used for the chemical source term? I think BDF 2 are mostly used, isn't it?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#16 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,273
Rep Power: 34   |
I think the better source would be this, Armfield has few papers about fractional solvers, I remember that later versions treated diffusion term implicitly while treating convective term explicit.
Their discussion about stability applies to your case. If you search papers with armfield and fractional solvers, there must be discussion about stability and time stepping. I am sorry I can not be more help because I read lots of papers etc and it is hard to remember which paper had what. PS: It is strange that I started my CFD career with combustion but have never coded what you are doing. |
|
|
|

|
|
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
Quote:
exactly, what do you mean for BDF 2? |
||
|
|

|
||
|
|
|
#18 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
I meant the Backward Differentiation Formula of step size 2 (BDF 2) - like here: https://en.wikipedia.org/wiki/Backwa...iation_formula
At the moment I am implementing the BDF1 that corresponds to the Backward Euler discretization.
__________________
Keep foaming, Tobias Holzmann Last edited by wyldckat; September 11, 2016 at 08:09. Reason: removed reference to removed post |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,764
Rep Power: 71    |
So, you are thinking to use the method of lines, you discretize the diffusion term in space and then solve the ODE system:
dYk/dt = D(Yk) + w(Yk) Since you are interested only to a steady state, I think that implicit multi-step methods such as Adams-Moulton can be feasible to work. But I am not sure if the usefal time step greater than for explicit (Adams-Bashforth) can be really useful, the time of the reaction can force you to use small time step. Using the splitting you can try first: dY*k/dt = w(Yk) the second stage being the solving for the diffusion, after that a sufficiently number of time step for the reaction have been solved to reach the characteristic diffusion time. The splitting reduces the time accuracy but it is quite good if you are not interested in following the time evolution ... Last edited by FMDenaro; September 7, 2016 at 15:58. |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
|
Typically, for non linear coupled equations you still need the jacobian to determine the maximum allowable time step. For each equation you get the maximum absolute eigenvalue of the jacobian and the max dt is something inversely proportional to that.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| what is swap4foam ?? | AB08 | OpenFOAM | 28 | February 2, 2016 01:22 |
| [Other] Adding solvers from DensityBasedTurbo to foam-extend 3.0 | Seroga | OpenFOAM Community Contributions | 9 | June 12, 2015 17:18 |
| OpenFOAM without MPI | kokizzu | OpenFOAM Installation | 4 | May 26, 2014 09:17 |
| [swak4Foam] Swak4FOAM 0.2.3 / OF2.2.x installation error | FerdiFuchs | OpenFOAM Community Contributions | 27 | April 16, 2014 15:14 |
| DecomposePar links against liblamso0 with OpenMPI | jens_klostermann | OpenFOAM Bugs | 11 | June 28, 2007 17:51 |