CFD Online Discussion Forums - pressure boundary conditions for collocated grid for Navier-Stokes

Page 1 of 2

Show 40 post(s) from this thread on one page

CFD Online Discussion Forums (https://www.cfd-online.com/Forums/)

- Main CFD Forum (https://www.cfd-online.com/Forums/main/)

- - pressure boundary conditions for collocated grid for Navier-Stokes (https://www.cfd-online.com/Forums/main/187563-pressure-boundary-conditions-collocated-grid-navier-stokes.html)

selig5576

May 9, 2017 15:38

pressure boundary conditions for collocated grid for Navier-Stokes

Assumptions:
1. Uniform equally spaced grid
2. 2D

When using the Chorin Projection method to solve the incompressible NS on a collocated grid we end up having to solve the following elliptic PDE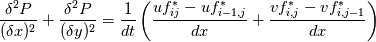

$\frac{\delta^{2} P}{(\delta x)^{2}} + \frac{\delta^{2} P}{(\delta y)^{2}} = \frac{1}{dt} \left(\frac{uf_{ij}^{*} - uf_{i-1,j}^{*}}{dx} + \frac{vf_{i,j}^{*} - vf_{i,j-1}^{*}}{dx} \right)$

where we have the face velocities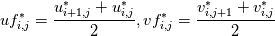

$uf_{i,j}^{*} = \frac{u^{*}_{i+1,j} + u^{*}_{i,j}}{2}, vf_{i,j}^{*} = \frac{v^{*}_{i,j+1} + v^{*}_{i,j}}{2}$

Our boundary conditions on all four sides are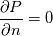
$\frac{\partial P}{\partial n} = 0$

When solving the pressure Poisson equation on the 4 boundaries is the procedure the same as if we were using the staggered grid? I've read some literature on it and I still don't quite understand if the pressure boundary conditions are treated differently. In my code I have

Code:

P(1,:) = P(2,:)

P(nx,:) = P(nx-1,:)

P(:,1) = P(:,2)

P(:,ny) = P(:,ny-1)

%Corners

P(1,1) = 1.0 % degree of freedom

P(nx,ny) = P(nx-1,ny-1) top right

P(nx,1) = P(nx-1,2) bottom right

P(1,ny) = P(2,ny-1) top left

Which gives me good results for the lid driven cavity, however according to http://www3.nd.edu/~gtryggva/CFD-Cou...re-15-2017.pdf
the pressure boundaries are treated differently. I was curious if my understanding of how to implement the pressure BCs on a collocated is correct. In my code I am using standard central differencing with extra treatment for the handling the ghost points.

FMDenaro

May 9, 2017 16:33

Actually, fixing the homogeneous Neumann BC, you have to correct the source term with the correct normal velocity components. Otherwise, the compatibility condition is not fulfilled.

I can suggest to have a look to the procedure I used here, you will find the answer to what you are asking for

https://www.researchgate.net/publica...y-driven_flows

https://www.researchgate.net/publica...taggered_grids

selig5576

May 9, 2017 17:16

Pressure BC

Hi Dr. Denaro,

Thank you for the two papers! In terms of the homogenous Neumann BC in Dr. Tryggva's code, is that what the u and v velocity terms are acting as? Upon first read I was quite confused.

FMDenaro

May 9, 2017 17:31

Quote:

Originally Posted by selig5576 (Post 648241)

Hi Dr. Denaro,

Thank you for the two papers! In terms of the homogenous Neumann BC in Dr. Tryggva's code, is that what the u and v velocity terms are acting as? Upon first read I was quite confused.

The slides show the interpolation introduced to manage the decoupling in the pressure grid when collocate arrangement is used. But you need to see the BC for pressure.

selig5576

May 11, 2017 19:02

Pressure BC

1 Attachment(s)

Hi,

Upon reading your paper, I am curious if you could provide some insight on the differences between your pressure BC and the ones from the slides. The one in your paper has velocity components v_(n+1) and v* however the one of in Tryggva's only has the v* component. Conceptually yours makes more sense, but I'm not quite grasping the idea of it enough to have a full understanding. Sorry for the stupid question.

FMDenaro

May 12, 2017 03:06

Quote:

Originally Posted by selig5576 (Post 648531)

As you can see, the relation used on the BC.s is nothing else that the discrete momentum equation arranged in the form of the Hodge decomposition. This way, the Neumann BC involves the real velocity component v_n+1 that is a known quantity on the wall. You prescribe it and in such a way you ensure the compatibility condition that is a required constraint to get one solution.

You can also see the BC in this way: once the homogeneous Neumann condition is set (d phy/dy=0) then you have v*=v_n+1 that you insert in the source term. Therefore, in the slides you have to consider the physical velocity component.

selig5576

May 12, 2017 14:40

Pressure BC

Hi Dr. Denaro,

Thank you for the excellent explanation, I will try both procedures. In terms of the corner boundary conditions, the pressure BC would be handled as follows (following the method from the slides)

Code:

P(1,ny) = P(2,ny-1) + (1/dt)*(dx*us(1,ny) + dy*vs(1,ny));

P(nx,ny) = P(nx-1,ny-1) + (1/dt)*(dx*us(nx,ny) + dy*vs(nx,ny));

P(nx,1) = P(nx-1,2) + (1/dt)*(dx*us(nx,1) + dy*vs(nx,1));

P(1,1) = 1.0;

I would imagine we would need us and vs since we are applying it in both x and y at the same time.

FMDenaro

May 12, 2017 15:03

Quote:

Originally Posted by selig5576 (Post 648683)

Code:

P(1,ny) = P(2,ny-1) + (1/dt)*(dx*us(1,ny) + dy*vs(1,ny));

P(nx,ny) = P(nx-1,ny-1) + (1/dt)*(dx*us(nx,ny) + dy*vs(nx,ny));

P(nx,1) = P(nx-1,2) + (1/dt)*(dx*us(nx,1) + dy*vs(nx,1));

P(1,1) = 1.0;

I would imagine we would need us and vs since we are applying it in both x and y at the same time.

You do not have to discretize the Neumann BC.s... just substitute the normal derivative into the equation for the nodes close to the frontiers, simplify the entries of the matrix and modify the source term.

selig5576

May 16, 2017 12:18

Pressure BC Rhie-Chow

Hi Dr. Denaro,

I think I am getting incorrect results and I believe it has to do with the way I'm handling the pressure BC. From what I have done in terms of your paper and from lectures here is how I am solving the PPE (using SOR)

Note:
$uf^{*}_{ij} = \frac{u^{*}_{i+1,j} + u^{*}_{i,j}}{2}$
Using SOR on the PPE we have
$P_{i,j} = (1-\omega)P_{ij} + \frac{\omega}{2/dx^{2} + 2/dy^{2}} \left(\frac{P_{i+1,j} + P_{i-1,j}}{dx^{2}} + \frac{P_{i,j+1} + P_{i,j-1}}{dy^{2}} - R_{i,j}\right)$

The R term is defined as

$\frac{\rho}{dt} \left(\frac{uf_{i,j}^{*} - uf_{i-1,j}^{*}}{dx} + \frac{vf_{i,j}^{*} - vf_{i,j-1}^{*}}{dy} \right)$

For the left boundary condition, i=1, we have
$P_{1,j} = (1-\omega)P_{1j} + \frac{\omega}{2/dx^{2} + 2/dy^{2}} \left(\frac{P_{2,j} + P_{0,j}}{dx^{2}} + \frac{P_{1,j+1} + P_{1,j-1}}{dy^{2}} - R_{1,j}\right)$

Since we have

$uf^{n+1}_{ij} = uf^{*}_{ij} - (dt/\rho) \left(\frac{P_{i+1,j} - P_{i,j}}{dx} \right)$
then at the boundary i=1 we have

$\frac{P_{2,j} - P_{1,j}}{dx} = \frac{1}{dt} \left(uf^{n+1}_{1,j} - uf^{*}_{1,j} \right)$

This is where I am having trouble understanding how to use the inhomgeneous neumann BC for the left-hand side of the PPE evaluated at i=1. From what I have seen people have evaluated the PPE at i=2, but I don't see how that solves the pressure equation at P(1,j). Thanks

EDIT 1:

I am currently using

$\frac{\partial P}{\partial n} = 0$

which means that if we use centered finite differences we get for the PPE

$P_{1,j} = (1-\omega) P_{1,j} + \frac{\omega}{2/dx^{2} + 2/dy^{2}} \left(\frac{1}{dx^{2}} 2*P_{2,j} + \frac{1}{dy^{2}}\left( P_{1,j+1} + P_{1,j-1}\right) - R_{1,j} \right)$

for R we have

$R_{1,j} = \frac{1}{dt} \left(\frac{uf^{*}_{1,j} - uf_{1,j}}{dx} + \frac{vf^{*}_{1,j} - vf^{*}_{1,j-1}}{dy} \right)$

We note that

$uf_{1,j} = \frac{u_{2,j} + u_{1,j}}{2}.$

The approach i'm using here I'm not confident is right.

FMDenaro

May 16, 2017 12:45

I give you an example for a 1D simple case:

d/dx(dp/dx) =(1/dt) du*/dx

with the Neumann BC (U is the known physical velocity on the boundary)
dp/dx = (1/dt) (u*- U)

Now consider that i=1 is a boundary and i=2 is the first node where you write the pressure equation.

X......X.....|.....X.....|..... FV grid
1......2............3......... i ordering

Discretize at i=2 the equation first in this way

(dp/dx|i=2+1/2 -dp/dx|i=1)/dx = (1/dt) (u*|i=2+1/2 - u*|i=1 )/dx

Now use the Neumann BC

dp/dx|i=1 =(1/dt)*(u*|i=1-U)

and substitute in the equation

(dp/dx|i=2+1/2)/dx = (1/dt) (u*|i=2+1/2-U )/dx

discretize

(p(3)-p(2))/dx^2 = (1/dt) ((u*(3)+u*(2))/2 -U)/dx

This is the equation for the node i=2 after inserting the non-homogeneous Neumann BC. As you can see, no u* on the boundary is required, only the physical velocity U.
You have no need to write the equation at i=1 where the BC is prescribed.

selig5576

May 16, 2017 15:35

Pressure BC

1 Attachment(s)

Hi Dr. Denaro,

That clears up a lot. Using SOR my implementation is

Code:

for j=2:ny-1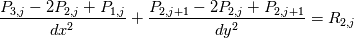

 R(2,j) = (rho/dt)*((1/dx)*(ufs(2,j) - u(1,j)) + (1/dy)*(vfs(2,j) - vfs(2,j-1)));

 P(2,j) = (1-omega)*P(2,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(3,j) + (1/dy^2)*(P(2,j+1) + P(2,j-1)) - R(2,j));



R(nx,j) = (rho/dt)*((1/dx)*(u(nx,j) - ufs(nx-1,j)) + (1/dy)*(vfs(nx,j) - vfs(nx,j-1)));

P(nx,j) = (1-omega)*P(nx,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(nx-1,j) + (1/dy^2)*(P(nx,j+1) + P(nx,j-1)) - R(nx,j));

end



for i=2:nx-1

R(i,2) = (rho/dt)*((1/dx)*(ufs(i,2) - ufs(i-1,2)) + (1/dy)*(vfs(i,2) - v(i,1)));

P(i,2) = (1-omega)*P(i,2) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,2) + P(i-1,2)) + (1/dy^2)*P(i,3) - R(i,2));

    

R(i,ny) = (rho/dt)*((1/dx)*(ufs(i,ny) - ufs(i-1,ny)) + (1/dy)*(v(i,ny) - vfs(i,ny-1)));

P(i,ny) = (1-omega)*P(i,ny) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,ny) + P(i-1,ny)) + (1/dy^2)*P(i,ny-1) - R(i,ny));

end

The way I formulated the PPE with SOR at the left (i=2) boundary is
$\frac{P_{3,j} - 2 P_{2,j} + P_{1,j}}{dx^{2}} + \frac{P_{2,j+1} - 2 P_{2,j} + P_{2,j+1}}{dy^{2}} = R_{2,j}$

Splitting up gives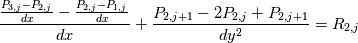

$\frac{\frac{P_{3,j} - P_{2,j}}{dx} - \frac{P_{2,j} - P_{1,j}}{dx}}{dx} + \frac{P_{2,j+1} - 2 P_{2,j} + P_{2,j+1}}{dy^{2}} = R_{2,j}$

Using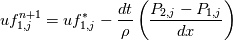

$uf^{n+1}_{1,j} = uf^{*}_{1,j} - \frac{dt}{\rho} \left(\frac{P_{2,j} - P_{1,j}}{dx} \right)$

We get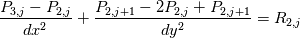

$\frac{P_{3,j} - P_{2,j}}{dx^{2}} + \frac{P_{2,j+1} - 2 P_{2,j} + P_{2,j+1}}{dy^{2}} = R_{2,j}$

Now I use SOR which gives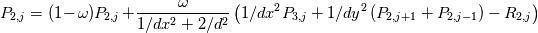
$P_{2,j} = (1-\omega) P_{2,j} + \frac{\omega}{1/dx^{2} + 2/d^{2}} \left(1/dx^{2} P_{3,j} + 1/dy^{2} \left(P_{2,j+1} + P_{2,j-1} \right) - R_{2,j} \right)$
I am under the impression I still have the solve the PPE at i=2, ny, j=2,ny but with the non-homogeneous Neumann BC and apply the correction to the RHS of the PPE. Thank you for the help Dr. Denaro!

EDIT: Looking at the pressure contour I notice the top left is different than that of the top right in the sense of the contours. Is that correct? With a staggered grid I don't believe I get that.

FMDenaro

May 16, 2017 15:53

1) For the lid driven cavity is correct that you have at corners a non-symmetric pattern, you have pressure increaing when the flow impact with the wall.
2) Depending on you formulation, you can end up with an approximate projection, that is the discrete divergence-free constraint is not driven to zero up to machine precision but only up to the local truncation error.
3) If you see the expression for the BC.s, it will be that same if you prescribe dp/dx=0 and u*=U (=0 for a wall) in the source term.
4) If the BC.s are correct, you do not need to prescribe any fixed value for the pressure, you can let SOR to set the constant. That will increas the rate of convergence.

selig5576

May 16, 2017 16:12

Pressure BC

Hi Dr Denaro,

1. Thats good to know that is supposed to happen in the corners.
2. Interesting
3. I will test it out
4. I am setting the pressure BC's manually as I am merely test the code on well known test problems. Eventually I will expand it to 3D and study more complexed problems.

In terms of the corners points P(nx,1), P(1,ny), P(nx,ny) I applied as follows

Code:

R(2,ny) = (rho/dt)*((1/dx)*(ufs(2,ny) - u(1,ny)) + (1/dy)*(v(1,ny) - vfs(2,ny)));

P(2,ny) = (1-omega)*P(2,ny) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(3,ny) + (1/dy^2)*P(2,ny-1) - R(2,ny));

           

R(nx,2) = (rho/dt)*((1/dx)*(u(nx,2) - ufs(nx-1,2)) + (1/dy)*(vfs(nx,2) - v(nx,1)));

P(nx,2) = (1-omega)*P(nx,2) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-1,2) + (1/dy^2)*P(nx,3) - R(nx,2));

           

R(nx,ny) = (rho/dt)*((1/dx)*(u(nx,ny) - ufs(nx-1,ny)) + (1/dy)*(v(nx,ny) - vfs(nx,ny-1)));

P(nx,ny) = (1-omega)*P(nx,ny) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-1,ny) + (1/dy^2)*P(nx,ny-1) - R(nx,ny));

I notice that on P(1,: ) its all zeros, is that supposed to occur? I assume thats due to the way the pressure BCs are formulated. Thanks! :)

FMDenaro

May 16, 2017 16:20

Quote:

Originally Posted by selig5576 (Post 649136)

Code:

R(2,ny) = (rho/dt)*((1/dx)*(ufs(2,ny) - u(1,ny)) + (1/dy)*(v(1,ny) - vfs(2,ny)));

P(2,ny) = (1-omega)*P(2,ny) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(3,ny) + (1/dy^2)*P(2,ny-1) - R(2,ny));

           

R(nx,2) = (rho/dt)*((1/dx)*(u(nx,2) - ufs(nx-1,2)) + (1/dy)*(vfs(nx,2) - v(nx,1)));

P(nx,2) = (1-omega)*P(nx,2) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-1,2) + (1/dy^2)*P(nx,3) - R(nx,2));

           

R(nx,ny) = (rho/dt)*((1/dx)*(u(nx,ny) - ufs(nx-1,ny)) + (1/dy)*(v(nx,ny) - vfs(nx,ny-1)));

P(nx,ny) = (1-omega)*P(nx,ny) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-1,ny) + (1/dy^2)*P(nx,ny-1) - R(nx,ny));

I notice that on P(1,: ) its all zeros, is that supposed to occur? I assume thats due to the way the pressure BCs are formulated. Thanks! :)

If you want to compute the pressure along the walls, you need to compute it explicitly from the Neumann BC after the SOR has reached convergence.

selig5576

May 16, 2017 16:39

Pressure BC

Hi,

Is it necessary to compute the pressure along the walls after P has reached convergence given I've already computed the pressure at the walls within the iteration process?.

FMDenaro

May 16, 2017 16:44

That's the point! In your SOR you have to compute only the equations for the internal unknowns and all these equations (once you substitute correctly the BC.s) have no nodes for the pressure at the walls! For this reason, only after you get the solution the pressure at the walls can be computed.

selig5576

May 17, 2017 11:31

Pressure BC

Hi Dr. Denaro,

I believe I have made a mistake in my code (correct me if i'm wrong.) If I care about the pressure at i=2 and j=2, then at the end points should it not be i=nx-1 and j=ny-1 instead of i=nx and j=ny. Upon imposing the non-homogenous Neumann BC at ny-1 and ny-1 I get 0s on all four sides and after my SOR iteration (outside the loop) I set P(1,: ) = P(2,: ), P(nx,: ) = P(nx-1,: ), P(:,1) = P(:,2), P(:,ny) = P(:,ny-1). I'm using backward/forward differencing for the Neumann BCs after I have iterated my pressure Poisson for the interior. I assume this is what you meant?

Code:

while (IterCntr == 0 && Iter <= IterMax)                

        for j=2:ny-1

            for i=2:nx-1

                P(i,j) = (1-omega)*P(i,j) + omega/(2/dx^2 + 2/dy^2)*((P(i+1,j) + P(i-1,j))/dx^2 + (P(i,j+1) + P(i,j-1))/dy^2 - R(i,j));

            end

        end

         

        for j=2:ny-1

            R(2,j) = (rho/dt)*((1/dx)*(ufs(2,j) - u(1,j)) + (1/dy)*(vfs(2,j) - vfs(2,j-1)));

            P(2,j) = (1-omega)*P(2,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(3,j) + (1/dy^2)*(P(2,j+1) + P(2,j-1)) - R(2,j));

     

            R(nx-1,j) = (rho/dt)*((1/dx)*(u(nx,j) - ufs(nx-2,j)) + (1/dy)*(vfs(nx-1,j) - vfs(nx-1,j-1)));

            P(nx-1,j) = (1-omega)*P(nx-1,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(nx-2,j) + (1/dy^2)*(P(nx-1,j+1) + P(nx-1,j-1)) - R(nx-1,j));

        end

 

        for i=2:nx-1

            R(i,2) = (rho/dt)*((1/dx)*(ufs(i,2) - ufs(i-1,2)) + (1/dy)*(vfs(i,2) - v(i,1)));

            P(i,2) = (1-omega)*P(i,2) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,2) + P(i-1,2)) + (1/dy^2)*P(i,3) - R(i,2));

    

            R(i,ny-1) = (rho/dt)*((1/dx)*(ufs(i,ny-1) - ufs(i-1,ny-1)) + (1/dy)*(v(i,ny) - vfs(i,ny-2)));

            P(i,ny-1) = (1-omega)*P(i,ny-1) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,ny-1) + P(i-1,ny-1)) + (1/dy^2)*P(i,ny-2) - R(i,ny-1));

        end

         

        R(2,ny-1) = (rho/dt)*((1/dx)*(ufs(2,ny-1) - u(1,ny-1)) + (1/dy)*(v(1,ny) - vfs(2,ny-1)));

        P(2,ny-1) = (1-omega)*P(2,ny-1) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(3,ny-1) + (1/dy^2)*P(2,ny-2) - R(2,ny-1));

           

        R(nx-1,2) = (rho/dt)*((1/dx)*(u(nx,2) - ufs(nx-2,2)) + (1/dy)*(vfs(nx-1,2) - v(nx,1)));

        P(nx-1,2) = (1-omega)*P(nx-1,2) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-2,2) + (1/dy^2)*P(nx-1,3) - R(nx-1,2));

           

        R(nx-1,ny-1) = (rho/dt)*((1/dx)*(u(nx,ny) - ufs(nx-2,ny-1)) + (1/dy)*(v(nx,ny) - vfs(nx-1,ny-2)));

        P(nx-1,ny-1) = (1-omega)*P(nx-1,ny-1) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-2,ny-1) + (1/dy^2)*P(nx,ny-2) - R(nx-1,ny-1));

        

        P(2,2) = 1.0; 

                

        E = P - POld;   

        normE = sqrt(sum(sum(E.^2)));

        error = normE/sqrt(nx*ny);  

         

        POld = P;

         

        if (error >= tol)

            Iter = Iter + 1;

        else

            IterCntr = 1;

        end

    end 

     

    P(1,: ) = P(2,: );

    P(nx,: ) = P(nx-1,: );

    P(:,1) = P(:,2);

    P(:,ny) = P(:,ny-1);

I assume since we have already solved for pressure then explicitly setting the Neumann BC is sufficient (as mentioned.)...

FMDenaro

May 17, 2017 11:47

I strongly suggest to use a different approach... Assume i=2,nx-1 and j=2,ny-1 are the internal pressure unknowns. You have to split the cycle for nodes where the unchanged Laplace (no BC.s) matrix entries and the unchanged source term are in effect: i=3,nx-2 and j=3,ny-2.
This way, you treat explicitly the nodes involving BC.s and write the modified SOR instructions both changing the matrix entries and the source term.

And the instructions P(1,: ) = P(2,: ), P(nx,: ) = P(nx-1,: ), P(:,1) = P(:,2), P(:,ny) = P(:,ny-1) correspond to homogeneous Neumann conditions. Actually, you are using non homegeneous ones....Note that dp/dn=0 is a boundary layer approximation.

My question is now: how do you compute the intermediate velocity v* on the boundaries?

selig5576

May 17, 2017 13:29

Pressure BC

If I understand you correctly, I need to change my indexing for the interior notes from 2:nx-1, 2:ny-1 TO 3:nx-2, 3:ny-2 so I can handle i=2,j=2,i=nx-1,j=ny-1.

The way I am calculating u* and v* is by explicitly setting it to the boundary, in this case 0 (except for us(:,ny).)

Code:

for j=3:ny-2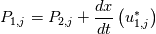

        for i=3:nx-2

            R(i,j) = (rho/dt)*((1/dx)*(ufs(i,j) - ufs(i-1,j)) + (1/dy)*(vfs(i,j) - vfs(i,j-1)));

        end

    end

 while (IterCntr == 0 && Iter <= IterMax)                

        for j=3:ny-2

            for i=3:nx-2

                P(i,j) = (1-omega)*P(i,j) + omega/(2/dx^2 + 2/dy^2)*((P(i+1,j) + P(i-1,j))/dx^2 + (P(i,j+1) + P(i,j-1))/dy^2 - R(i,j));

            end

        end

         

        for j=3:ny-2

            R(2,j) = (rho/dt)*((1/dx)*(ufs(2,j) - u(1,j)) + (1/dy)*(vfs(2,j) - vfs(2,j-1)));

            P(2,j) = (1-omega)*P(2,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(3,j) + (1/dy^2)*(P(2,j+1) + P(2,j-1)) - R(2,j));

     

            R(nx-1,j) = (rho/dt)*((1/dx)*(u(nx,j) - ufs(nx-2,j)) + (1/dy)*(vfs(nx-1,j) - vfs(nx-1,j-1)));

            P(nx-1,j) = (1-omega)*P(nx-1,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(nx-2,j) + (1/dy^2)*(P(nx-1,j+1) + P(nx-1,j-1)) - R(nx-1,j));

        end

 

        for i=3:nx-2

            R(i,2) = (rho/dt)*((1/dx)*(ufs(i,2) - ufs(i-1,2)) + (1/dy)*(vfs(i,2) - v(i,1)));

            P(i,2) = (1-omega)*P(i,2) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,2) + P(i-1,2)) + (1/dy^2)*P(i,3) - R(i,2));

    

            R(i,ny-1) = (rho/dt)*((1/dx)*(ufs(i,ny-1) - ufs(i-1,ny-1)) + (1/dy)*(v(i,ny) - vfs(i,ny-2)));

            P(i,ny-1) = (1-omega)*P(i,ny-1) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,ny-1) + P(i-1,ny-1)) + (1/dy^2)*P(i,ny-2) - R(i,ny-1));

        end

         

        R(2,ny-1) = (rho/dt)*((1/dx)*(ufs(2,ny-1) - u(1,ny-1)) + (1/dy)*(v(1,ny) - vfs(2,ny-1)));

        P(2,ny-1) = (1-omega)*P(2,ny-1) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(3,ny-1) + (1/dy^2)*P(2,ny-2) - R(2,ny-1));

           

        R(nx-1,2) = (rho/dt)*((1/dx)*(u(nx,2) - ufs(nx-2,2)) + (1/dy)*(vfs(nx-1,2) - v(nx,1)));

        P(nx-1,2) = (1-omega)*P(nx-1,2) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-2,2) + (1/dy^2)*P(nx-1,3) - R(nx-1,2));

           

        R(nx-1,ny-1) = (rho/dt)*((1/dx)*(u(nx,ny) - ufs(nx-2,ny-1)) + (1/dy)*(v(nx,ny) - vfs(nx-1,ny-2)));

        P(nx-1,ny-1) = (1-omega)*P(nx-1,ny-1) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-2,ny-1) + (1/dy^2)*P(nx,ny-2) - R(nx-1,ny-1));

        

        P(2,2) = 1.0; 

                

        E = P - POld;   

        normE = sqrt(sum(sum(E.^2)));

        error = normE/sqrt(nx*ny);  

         

        POld = P;

         

        if (error >= tol)

            Iter = Iter + 1;

        else

            IterCntr = 1;

        end

    end

You are correct in terms of the Neumann BC not being homogeneous. In that case:

$P_{1,j} = P_{2,j} + \frac{dx}{dt} \left(u^{*}_{1,j} \right)$

Similar to that of the slides in my earlier posted? By my understanding, by having my loops, 3:nx-2 and 3:ny-2, I am able to correctly solve the PPE at the boundarys i=2,i=nx-1,j=2,j=ny-1 and then finally (after I have iterated P) i=1,j=1,i=nx,j=ny.

Thank you for the patience, I don't know why this is so hard for me to grasp :confused:

FMDenaro

May 17, 2017 14:02

I give an example of pseudo-code

i=2;j=2 (2 BC.s)
p(i,j)=..
j=2 (1 BC)
for i=3,nx-2
p(i,j)=...
end
i=nx-1;j=2 (2 BC.s)
p(i,j)=..

for j=3,ny-2
i=2 (1 BC)
p(i,j)=..
i=nx-1
p(i,j)=--
end

and so on..

The setting of u* and v* is somehow complex and depends on the accuracy you want to treat the time integration.
Setting u*=v*=0 on the walls is equivalent to set dp/dn=0 ...
Have you read some literature about this issue?

All times are GMT -4. The time now is 00:30.

Page 1 of 2

Show 40 post(s) from this thread on one page