 |
|
|
[Sponsors] | |||||
Understanding Davis artificial viscosity |
 5Likes
5Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
I'm solving 2D Euler's equations in Cartesian coordinates:
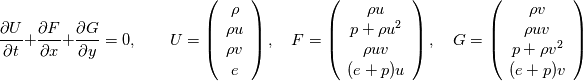 using finite difference MacCormack method with Davis artificial viscosity which dampens non-physical oscillations. The MacCormack method is pretty simple and not shown here. Davis viscosity works good in my simulations, but is quite difficult; I'm trying to fully understand it in order to apply it cylindrical coordinates later. I hope that some of you may help me with unclear parts of it (shown in bold font below). Viscous terms are added after 2nd MacCormack step as follows (formulated in 1D for simplicity):  where  denote field values (at denote field values (at  -th coordinate point and -th coordinate point and 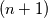 -th time layer) calculated by MacCormack scheme as usual, and -th time layer) calculated by MacCormack scheme as usual, and 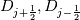 , are forward and backward differences of U with non-linear coefficients: , are forward and backward differences of U with non-linear coefficients: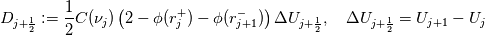 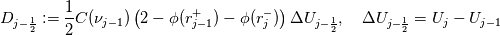 Where 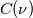 is a limited coefficient based on Courant number: is a limited coefficient based on Courant number: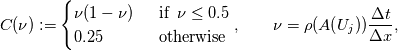 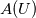 is the Jacobian matrix of vector is the Jacobian matrix of vector 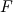 , , 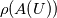 is it's spectral radius (for Euler's equations it equals is it's spectral radius (for Euler's equations it equals 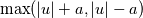 , where , where  is the speed of sound). is the speed of sound).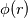 is simple limiting function: is simple limiting function: 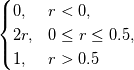 And finally 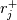 , ,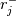 are slope ratios: are slope ratios: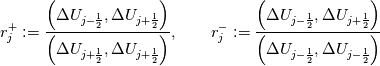 Where 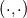 is scalar product. These ratios are positive in monotone areas and negative in non-monotone areas, so that in general coefficients like is scalar product. These ratios are positive in monotone areas and negative in non-monotone areas, so that in general coefficients like 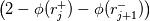 are equal 2 in non-monotone areas; about 1 in monotone, but "curvy" areas; and equal 0 in monotone (and rectilinear) areas. are equal 2 in non-monotone areas; about 1 in monotone, but "curvy" areas; and equal 0 in monotone (and rectilinear) areas.If both these ( 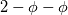 ) coefficients are equal 2, and both ) coefficients are equal 2, and both 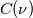 are equal 0.25 we have an effective second derivative of the field value: are equal 0.25 we have an effective second derivative of the field value: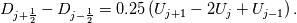 But where is the division by 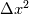 ? If the viscosity would be simply the 2nd derivative, the scheme would look like ? If the viscosity would be simply the 2nd derivative, the scheme would look like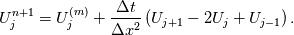 Is 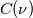 effectively equals effectively equals 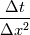 ? ?And, what if 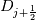 is non-zero and is non-zero and 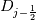 is zero? Does it still yield an effective 2nd derivative? is zero? Does it still yield an effective 2nd derivative?
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
I think you should see the artificial viscosity as a term that disappears as dx->0. Therefore, multiply and divide by dx^2 and you get a second order derivative multiplied by dx^2.
You wrote dt/dx^2 but the dimensions are no longer congruent |
|
|
|

|
|
|
|
|
#3 | |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
Thanks for such a fast answer, FMDenaro!
Quote:
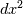 ? ?But spurious oscillations do not disappear as 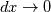 . If artificial viscosity disappears as . If artificial viscosity disappears as 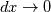 , how would it dampen the oscillations then? , how would it dampen the oscillations then?I can't say that I understand that completely. Could you elaborate? |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
The artificial viscosity has nothing to do with the physical viscosity. It is just an added terms that has the aim of dumping oscillations. But it has to be consistent with the original PDE equation as h->0.
I suggest a reading in the fundemental textbooks about the numerical solution of Euler equations. |
|
|
|

|
|
|
|
|
#5 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
Yeah, it seems that deep diving into the theory is inevitable :-)
Thanks again! |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Martin Hegedus
Join Date: Feb 2011
Posts: 500
Rep Power: 19  |
As a general statement, artificial viscosity is a consequence of numerical differentiation. It is not a physical term. It can be determined, in a hand waving way, from the wave equations. In a nutshell, central difference is a result of taking the limit when coming from the right and left.
In a sense, dF/dx is a function of lim (+ and -)->0 [dF/dx(+) + dF/dx(-)] + lim (+ and -)->0 [dF/dx(+) - dF/dx(-)]. If everything was perfect, and assuming no discontinuities, [dF/dx(+) - dF/dx(-)] would be zero. But numerically it is not. Thus the C*(U(i+1)-2*U(i)+U(i-1)) where C is a knob. |
|
|
|

|
|
|
|
|
#7 | |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
Quote:
"Knob" has too many meanings in English language, so I can't understand the meaning of this phrase :-) |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
I suggest having a reading to the texbook of Leveque (for example pag.71-72) to start with the concept of artificial viscosity explicitly added to the discretization in order to dump oscillations and numerical viscosity present in the local truncation error that is implicitly induced by the discretization.
|
|
|
|

|
|
|
|
|
#9 | |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
Quote:
|
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
||
|
|

|
|
|
|
|
#11 | |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
Quote:
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Problem with divergence | TDK | FLUENT | 13 | December 14, 2018 06:00 |
| How can use MacCormack & Baldwin artificial viscosity in term of generalized nonortho | Nam Tran Ha | CFD Freelancers | 0 | December 21, 2016 03:31 |
| Artificial viscosity | rads | CFX | 2 | July 31, 2006 07:02 |
| artificial viscosity | rvndr | Main CFD Forum | 1 | March 2, 2004 10:24 |
| Artificial Viscosity | Girish Bhandari | Main CFD Forum | 5 | January 13, 2001 13:22 |