
 |
It seems that I was misunderstanding how the flux is reconstructed:
My idea was to reconstruct base values - 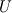 (or (or 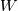 if we are performing characteristic decomposition) - and then substitute them to formulas of if we are performing characteristic decomposition) - and then substitute them to formulas of 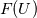 (or (or 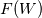 ) to obtain reconstructed fluxes. ) to obtain reconstructed fluxes. It looks like the correct way is to apply reconstruction procedure to 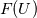 (or (or 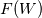 which is obtained by transformation which is obtained by transformation 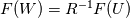 ) itself. Some quick tests I performed with this approach show very plausible results. ) itself. Some quick tests I performed with this approach show very plausible results. |
Hi there,
Here's what I am doing: after reconstructing the characteristic variables at the face, I use the left eigenvector matrix to convert them back to primitive variables. Then, I use these to compute the flux using the flux function, e.g. Lax-Friedrich method. It has performed well in several 1D test cases. USV |
| All times are GMT -4. The time now is 06:52. |