 |
|
|
[Sponsors] | |||||
Temporal convergence of RK method on shock tube problem |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Hi,
I tried to find the rate of convergence of RK (SSPRK2) method for Sod shock tube problem by plotting the log of error vs log of the number of temporal points. The error is calculated by finding the difference between the analytical solution at a point in x-axis (length) and numerical solution at that point but I didn't get any temporal convergence! but the solution is correct. I checked spatial convergence where I got first order. I checked the convergence of the SSPRK2 method on simple ODE where I got 2 but for Euler equation, I'm not getting any convergence in temporal discretization. Am I making any mistakes? or is it normal? Could you suggest some paper where the temporal convergence of RK methods is evaluated for Euler equation? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
What kind of norm are you using? For smooth solution it makes sense a convergence Analysis but here you have to consider the singularity.
Since you have first order accuracy, if you vary only the dt while taking constant h you must be sure that h is very small otherwise the spatial Terni in the truncation error causes a non-convergent error slope |
|
|
|

|
|
|
|
|
#3 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
I used manhattan norm (first norm). I sum up error in all the time step at a point and dived that by the number of time step and got a constant value over time step refining. This is strange and means zero convergence over the time iteration! The number of grid points that I used in spatial is 800. I guess this is more than enough. The number of time steps I used are [1749 1749*2 1749*4 1749*8]. Instead of summing up all the time I tried that at a point time and space that too gave a constant error! I feel that I'm making some mistake somewhere.
|
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
800 nodes gives you what h value? you have O(h) so as soon as you have dt<=O(h) you cannot see any correct convergence. I suggest using the L2 norm. YOu can also try the one-step analysis However, be aware that a real accuracy study requires a smooth solution. |
||
|
|

|
||
|
|
|
#5 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Quote:
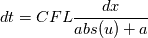 so dt will be much smaller than dx. I know my solution is not smooth but I expect at least first order convergence like spatial here. I tried with L2 norm too getting zero convergence as L1 norm so dt will be much smaller than dx. I know my solution is not smooth but I expect at least first order convergence like spatial here. I tried with L2 norm too getting zero convergence as L1 norm
|
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
if your range of dt values starts already below the O(h) you cannot see the correct convergence since the erro is dominated by the constant spatial term... try using a much more refined grid and start with dt higher. For using norm on non regular solution have a look to the paragraph in the book of Leveque on hyperbolic systems |
||
|
|

|
||
|
|
|
#7 |
|
Super Moderator
|
You are using explicit scheme so dt = O(dx) by CFL condition. When you do dx refinement, you are also refining dt. So that test already shows the temporal convergence.
Your error would be of the form 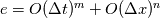 and if dt = O(dx) then  If you want to capture the value of m from the error, then you need to use 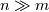 but this is possible only for smooth solutions. but this is possible only for smooth solutions.Regarding measuring the error, you can measure the error at some final time in some norm 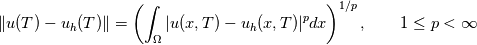 with 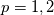 being common norms, and p=1 is more suitable for discontinuous solutions. being common norms, and p=1 is more suitable for discontinuous solutions.You could also take maximum over time 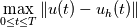 but this is a very strong norm and not suitable for discontinuous solutions. Instead you should measure in some weaker norm like 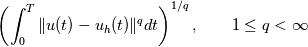 with q=1 being suitable for discontinuous solutions. For discontinuous solution, you get convergence rate of 0.5 in L1 norm and 0.25 in L2 norm. You can see this for the linear advection equation by running my code https://github.com/cpraveen/numpde/b...yp1dperconv.py Code:
$ python linhyp1dperconv.py -N 40 80 160 320 -scheme FTBS -ic hat Running for cells = 40 Running for cells = 80 Running for cells = 160 Running for cells = 320 N L1 rate L2 rate max rate 80 5.699071e-02 0.511890 1.316410e-01 0.270837 5.374514e-01 -0.027954 160 4.005457e-02 0.508760 1.091704e-01 0.270026 5.165374e-01 0.057261 320 2.826315e-02 0.503045 9.129933e-02 0.257906 5.023860e-01 0.040077 For a smooth solution, you get a rate of 1 in all norms Code:
$ python linhyp1dperconv.py -N 40 80 160 320 -scheme FTBS -ic smooth Running for cells = 40 Running for cells = 80 Running for cells = 160 Running for cells = 320 N L1 rate L2 rate max rate 80 1.551323e-02 0.989236 1.725378e-02 0.996692 2.439983e-02 0.997061 160 7.811945e-03 0.989745 8.680653e-03 0.991037 1.227636e-02 0.990988 320 3.919312e-03 0.995081 4.353772e-03 0.995538 6.157152e-03 0.995548 |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
That's the key, he does not use a constant CFL. As I have written before, taking h constant and varying dt makes the CFL variable. Since the local truncation error is a function L=L(h,dt) that means you are moving at h=const. along the L-surface. And to see the convergent slope you need that h is taken smaller than the smallest dt used in the convergence analysis. This happens on smooth solution, thus a more complicated situation happens for solution with singularity
|
|
|
|

|
|
|
|
|
#9 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Both of u emphasizing dt >> dx to make temporal convergence reliable. This is a valid point but I can't make it in Sod shock tube problem because of CFL constraint. I have a reasonably ok result with CFL number around 2 with one of the optimized RK4 methods even that can't make dt>>dx. I hope even higher stage RK optimized for stability can push it but I'm not sure. To make dt>dx I need CFL > 7 but I'm not aware of any explicit multistage method that can make it.
I have noticed that my normalized error by the number of time step is more or less constant over refining?. I hope it is trying to say something but I'm unable to understand it. |
|
|
|

|
|
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
|
||
|
|

|
||
 |
| Tags |
| convergence check, runge kutta method, time integration |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Solution of SOD Shock Tube Problem by using HARTEN Modified Flux TVD Scheme | xue sheng | Main CFD Forum | 5 | August 27, 2022 07:06 |
| Two solutions of Sod's shock tube problem | orxan.shibli | Main CFD Forum | 14 | May 20, 2016 21:41 |
| HLL Riemann Shock Tube Matlab Problem | Luke F | Main CFD Forum | 2 | May 20, 2016 02:10 |
| What's the boundary condition for 1D Shock Tube Problem? | Accelerator | Main CFD Forum | 0 | August 26, 2012 15:52 |
| shock tube: problem initiation | Gareth | Siemens | 3 | April 15, 2003 03:23 |