
 |
In your case, the discrete momentum equation is explicit and you have no particular problem in setting an initial condition for Pn. Be careful to the BC.s.
Have a look to this paper http://129.81.170.14/~cortez/Prints/accproj.pdf |
Practical implementation of projection method
1 Attachment(s)
I have recently read this very paper. For pnew, phi, and p, I am setting them to be initially 0. When I set pnew = p + phi I am not applying anything boundary condition to pnew or p. I only apply a BC for phi for the pressure poisson equation. Given p^n is the previous time level of p^n+1 shouldnt I set p^n = p^n+1 for the pressure update?
In terms of the paper I'm following I am studying this paper: http://www.math.tamu.edu/~guermond/P...o_jcp_2009.pdf |
Quote:
What do you mean for "I am not applying anything boundary condition to pnew or p"? Depending on the type of collocation, you might need to prescribe the values at the boundaries to compute the correct gradients to correct the velocity. I suggest to do simple test and running the code in debugging only for the first time step. Check that the divergence-free constraint is ensured at the end of the time step cell-by-cell. |
Projection Method
What I meant was I only apply
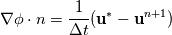 to to 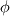 . Not Pnew or Pn. I am trying a collocated arrangement and I am not getting a divergence free velocity field (up to machine precision.) I believe what I am getting is results to that of an approximate projection method. My velocity profile looks correct, but my pressure profile does not seem to be right. . Not Pnew or Pn. I am trying a collocated arrangement and I am not getting a divergence free velocity field (up to machine precision.) I believe what I am getting is results to that of an approximate projection method. My velocity profile looks correct, but my pressure profile does not seem to be right. |
Quote:
|
Finally, consider that in the non-staggered grids some wiggles can be produced, for example see https://www.researchgate.net/publica...y-driven_flows
|
Boundary condition for Pnew
Yes, this is one of the frustrations I am finding in using a collocated arrangement and a compact stencil for pressure. May I ask you what I should prescribe to Pnew at the boundaries to get the correct pressure gradient profile?
|
When you write the increment [
at the boundary you should consider that the normal derivative on phi was prescribed to be zero therefore you can use the relation d Pn+1/dn = d Pn/dn. However, I think that this is the reason why you get a numerical boundary layer in the pressure field as reported by several papers. Unfortunately I use the pressure-free projection, not the incremental, therefore withour a direct experience I should better think about the use of the Hodge decomposition to avoid such problem. |
Projection Method
I appreciate your help professor Denaro! I was curious: For DNS or LES do people still use staggered grids in light of the problems of collocated grids?
|
Quote:
|
Pressure free projection method vs incremental projection method
I have been doing some readings on your papers with regards to pressure-free projection methods. It has led me to reading some papers by Kim and Moin. With regards to their statement of the "actual pressure"
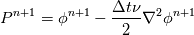 do I apply 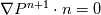 to P^{n+1} on the boundary or can I leave this term without any boundary treatment. Their paper is not very clear. Thank you! to P^{n+1} on the boundary or can I leave this term without any boundary treatment. Their paper is not very clear. Thank you! |
Quote:
You have to be careful of the fact that such relation appears only when you use the implicit Crank-Nicolson time integration. In your method this relation does not apply. However, rigorously speaking, the Neuman BC.s are just the projection of the Hodge decomposition along the normal direction. This is valid for any type of projection method. |
Pressure-free PM
I agree, in my case P^{n+1} = \phi^{n+1} as I am using FE integration. I quickly changed my solver to a pressure-free method and I update my pressure as follows
Code:
for j=1:nyCode:
for j=2:ny-1 |
Quote:
|
I forgot to mention that the method in the paper of Kim and Moin uses a staggered grid
|
Pressure profile
1 Attachment(s)
So after reading the paper by Brown. I noticed that
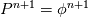 gives reduced accuracy as opposed to update pressure at the gives reduced accuracy as opposed to update pressure at the 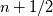 time level. As such I have time level. As such I have 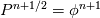 (i.e. I pressure update before I perform the corrector step) As such, my pressure profile is shown below. Since the paper by Moin used a staggered arrangement, I am under the impression I will get slightly less accurate results than that of the staggered mesh. (i.e. I pressure update before I perform the corrector step) As such, my pressure profile is shown below. Since the paper by Moin used a staggered arrangement, I am under the impression I will get slightly less accurate results than that of the staggered mesh. I have come across that there exists an improvement of the Rhie-Chow interpolation, titled "Improved Rhie-Chow Interpolation for Unsteady Flow Computations." Unfortunately, I do not have access to this paper, would this possibly increase the accuracy of my code? In the original paper by Rhie and Chow, it is used for a steady state turbulence problem. |
Your questions implies several issues... And for each one the answer is not simple to explain here.
1) Despite of what stated in the paper of Brown et al., the accuracy of the pressure-free projection method (be careful that here one refers as only to the time accuracy of the splitting method) can be high as you want. You need to consider the proper BC.s for the intermediate velocity. Then pressure can be recovered from phi. 2) The staggered grid in the paper of Kim and Moin is associated to a classical second order discretization that allows to get an exact projection method. Non-staggered grids with second order discretization have the problem of non-communicating grids for the pressure equation (large stencil) if you perform an exact projection method. Therefore, generally the approximate projection method is used on a compact stencil. However, the spatial accuracy is formally the same. 3) The R-C interpolation does not increase the order of accuracy. It is used to get a strong coupling. You can see also the discussion in the book of Peric and Ferziger. However, I just want to alert you abouyt the fact that the deeper and often hidden details of the projections methods have taken me engaged for some years... |
Projection Methods
Thank you for letting me pick your brain :D. I did not mean that the Rhie-Chow interpolation increases the accuracy of the method. What I was trying to get at is the improved Rhie-Chow method will provide a more stable solution for unsteady flow computations.
I just want to pick your brain on one other thing. So the BCs for the intermediate velocity step is a source of ambiguity for pressure-free PMs. To get second-order accuracy Moin proposed 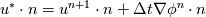 . In my current solver I have implemented CN-AB2. I only have one phi variable and that is the n+1 time level. Is that sufficient to just use n+1 in place of the n level for the BC? In a practical implementation I'm not sure how one would have . In my current solver I have implemented CN-AB2. I only have one phi variable and that is the n+1 time level. Is that sufficient to just use n+1 in place of the n level for the BC? In a practical implementation I'm not sure how one would have 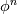 using an SOR type iterator as it only uses one variable. using an SOR type iterator as it only uses one variable. |
Quote:
Well, first the problem of the BC.s for the intermediate velocity exists only when using an implicit time integration. Then, the formulation proposed by Kim and Moin is actually only first order accurate therefore decreases the accuracy order close to a boundary. Now, the evaluation of the pressure field (or phi) in time has to be carefully considered. Consider for example the momentum equation (convection and diffusion is denoted by R) dv/dt + grad p = R, let integrate exactly in time vn+1-vn + Int [tn,tn+1] grad p dt = Int [tn,tn+1] R dt (1) Now we introduce an implicit discretization in R and disregard the pressure term v*-vn = Int_dis [tn,tn+1] R* dt (2) and, after the Poisson equation allows to solve for the field phi we can write vn+1=v* - dt*grad phi (3) If you substitute in this relation the equation (2) for the intermediate field vn+1-vn + dt*grad phi = Int_dis [tn,tn+1] R* dt (4) Now, comparing (1) and (2), you see that grad phi is actually correlated to a the time averaging in the interval tn,tn+1, is not a function evaluated at a certain time. If you are interested in the details of the formulation I analysed some years ago, you will find useful these papers: https://www.researchgate.net/publica...ary_conditions https://www.researchgate.net/publica...ection_methods https://www.researchgate.net/publica...blicationTitle |
| All times are GMT -4. The time now is 03:55. |