
 |
Well, there are some issues to discuss. First, look at the local truncation error of your discretization:
LTE=-0.5*dt*(a^2*d2u/dx^2-2*a*b*d3u/dx^3+b^2*d4u/dx^4) +... and, I am right, you have a higher order term in the form dx^3/dt (try to develop the LTE). Therefore, for fixed dx and vanishing dt you should get an increasing in the error. This is due to the fact that you need convergence for dx and dt going both to zero. Second, you cannot use a Dirac initial function to test such PDE as it is a non regular function. |
Quote:
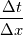 , which still leads to decreasing with smaller , which still leads to decreasing with smaller 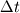 . Maybe some minor mistake in it? . Maybe some minor mistake in it? |
Quote:
I wrote only the term of O(dt), of course you have also terms of O(dx^2). The LTE is determined by substituting the Taylor expansion in time and space in your FTCS scheme. You can do it by hand, is a bit long to manage, or you can use Maple. However, you cannot use the Dirac as initial condition and the study of the convergence requires to use dt/dx->0 |
Quote:
Anyway, I wrote out the formula for LTE only with leading order terms (probably some mistakes in those coefficients): 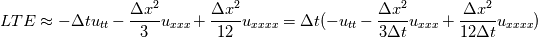 so by lowering the time step size, the LTE for time derivative would not increase, but the LTE for spatial derivative will. So which means it will increase the spatial error, and it appears to be like diffusion. Am I correct? |
As you see, if dx is taken constant while dt is diminished, you have both a dispersion and dissipation effects. However, you should still expand d2u/dt^2 using the PDE equation
|
Quote:
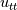 using the PDE equation"? Do you actually mean by using the PDE equation"? Do you actually mean by 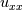 instead instead 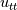 ? ? |
|
|
|
Quote:
|
Again, you see that using the Taylor expansion requires the solution to be regular...
|
Quote:
|
Quote:
Also from a numerical point of view, on a grid of size h the smallest wavelength you can represent is 2*h and that requires to describe a sine by using at least three grid points. |
Quote:
I have been trying to manage all the terms, and here is what I get 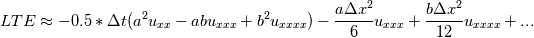 but it seems the 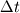 only affect those terms in the brackets; can't see any terms in the form of only affect those terms in the brackets; can't see any terms in the form of 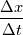 I am confused again... |
I should check all the procedure, I remember some further terms...
|
Quote:
|
1 Attachment(s)
Quote:
|
1 Attachment(s)
Quote:
|
1 Attachment(s)
I checked in my old notes and I extracted the LTE expression, it appears clearly that, provided that the dx allows to get the Reynolds cell number <=2, you have a global positive diffusion coefficient.
Now the issue is that if you compare the solution at some time T, when you decreases the time step you need more iteration to reach that time and the error effects summ. |
| All times are GMT -4. The time now is 04:37. |