
 |
jacobian block for implicit solver with non explicit flux function
Hello,
I am coding implicit finite volume. I have a doubt on how to construct a jacobian block associated to a face boundary which does not have an explicit form. The flux is of the form F(Q*) where Q* is the solution to a non linear equation solved numerically with Newton and which depends on Qint. I need dF/dQint. I'd like to avoid local finite differencing and stick to formal differentiation. Anyone has an idea ? I guess this situation appears as well for the differentiation of the Godunov flux with exact Riemann solver, if someone ever tried to do this. Thanks ! |
If you think about wall functions, I guess, they are not much different from what you want to do.
Only, note that, typically, one does not differentiate with respect to Qint (assuming with Qint you refer to the variable on the face), but with respect to the variable in the adjacent fluid cells (that is, with respect to your actual independent variables). In general, with WF, you would tipically express them as a classical, no WF, linear contribution + a correction with respect to it, and differentiate with respect to the linear contribution only. This general approach is know as deferred correction and is also used for convection schemes, anything of order higher than 1 (including diffusion), whatever you would be otherwise forced to discretize explicitly. Obviously, this only makes sense if the part you account for implicitly is somehow still related to the whole term. Note that, when implemented within a straight newton linearization, what you actually do is: - just use the full intended term in the explicit residual on the RHS - use your best approximation in the jacobian on the LHS and at convergence, whatever the approximation in the jacobian was, it has no more effect. |
Many thanks Sbaffini for your explanations. I am going to reformulate, to check if I understood.
Let's assume a cell centered 1st order FV to make things simpler. At the face boundary I have the constant average state Qint coming from the adjacent cell in the computational domain and known independant boundary data Qbc. The boundary condition consists of non linear relations, which give me a face vector Qf through the solution of a problem G(Qf,Qint,Qbc)=0. Then the final flux is computed F(Qf) and added to the RHS. Then you suggest linearizing Qf about Qint such that Qf=Qint+other terms. Then F(Qf) is approximately F(Qint) and take dF(Qint)/dQint as the Jacobian block contribution. This is a great complexity reduction but I am wondering how much information I loose in the process. Thank you for your time :) |
|
As suggested by praveen, you actually need dF/dQint itself as Jacobian block contribution, NOT dF/dQf (Q* in praveen answer), and this block contribution goes to the cell relative to Qint.
Still, while the form used by praveen is the mathematically correct one, I guess you should take control of dN/dQ*, in case it might become 0. Remember that the whole point in making things implicit is to then have a nice matrix, even if not accurate. |
Many thanks for your answers !
As a matter of fact, I use automatic differentiation to propagate derivatives with respect to the conservative variables. As I implemented this procedure with the goal of not worrying about complex flux functions or eos, I was having a doubt about its usability in this precise scenario where the function is not explicit. In this case, the derivatives are propagated through the whole Newton iterative scheme and I am wondering if I get at convergence (based on the norm of N) something even close to the analytic expression given by praveen. I guess I would have to derive by hand these expressions, or more safely use formal calculus software. I don't feel very confident in using finite differencing for checking purpose would you ? Sbaffini: if dN/dQ*=0 then the Newton scheme may stall to a local extremum, in that case I switch to a bracketed dichotomy algorithm |
What I meant is that, in the solution provided by praveen for dF/dQint, it might happen that your solution for N=0 ends up having also dN/dQ* = 0. You can use a bisection method to find the solution for N=0, but what about (dN/dQ*)^-1 in the formula for dF/dQint if that is the actual correct solution?
Of course, your problem can be such that a correct solution to N=0 never happen to also have dN/dQ*=0, but noting that you have a backup algorithm, I suspect that might not be the case. Also, not an expert here, but I guess that automatic differentiation algorithm would exactly replicate any unboundedness in the original jacobian; do you have a backup also for that? |
You can solve for
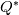 from from 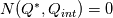 only if only if 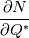 is invertible. This is impicit function theorem is invertible. This is impicit function theoremhttps://en.wikipedia.org/wiki/Implicit_function_theorem If that jacobian is singular, that means your problem 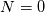 is ill-posed and you have to fix it at a mathematical/modeling level. It is not a numerical issue. is ill-posed and you have to fix it at a mathematical/modeling level. It is not a numerical issue. |
Well, ill-posedness happens nonetheless. Also, quoting from the link, the implicit function theorem gives a sufficient condition to ensure that there is such a function.
It is plenty of nonlinear problems whose solutions are in points of null derivatives. I don't think you can arbitrarily ban them from the physics just because of that. I think it is our math that should put them in a well posed manner if possible at all, or try to exclude those ill-posed solutions from the set of reachable ones. |
| All times are GMT -4. The time now is 16:35. |