 |
|
|
[Sponsors] | |||||
CFL condition for 2D Compressible Euler equations |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 10  |
Hi everyone,
I am currently coding a 2D solver for the compressible Euler equations. Prior to this I coded a 1D solver and it works like a charm, however I am running into issues for the 2D version. In terms of my method I am using the Local Lax Friedrichs method, or "Rusanov method." After a couple days of trying to figure out the problem I believe it has to do with the way I'm calculating my CFL condition. For my 1D problem I calculate the CFL condition for my time step size or "dt" as follows: 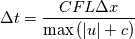 For the 2D problem (according to E.F. Toro) you would calculate dt as follows: 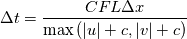 When I run my code it only plots the initial condition (t = 0). In terms of my time update, it works as I am using the 'same' procedure as for the 1D case. I have included the code below. If someone could assist that would be greatly appreciated. Code:
nx = 101;
dx = 1/(nx-1);
ny = 101;
dy = 1/(ny-1);
r = zeros(nx,ny);
u = zeros(nx,ny);
v = zeros(nx,ny);
E = zeros(nx,ny);
p = zeros(nx,ny);
x = zeros(nx,ny);
y = zeros(nx,ny);
Q = zeros(nx,ny,4);
Qnew = zeros(nx,ny,4);
F = zeros(nx,ny,4);
G = zeros(nx,ny,4);
Fh = zeros(nx-1,ny,4);
Gh = zeros(nx,ny-1,4);
gamma = 1.4;
c = zeros(nx,ny);
ah1 = zeros(nx,ny);
ah2 = zeros(nx,ny);
CFL = 0.5;
tMax = 0.25;
for j=1:ny
for i=1:nx
x(i,j) = (i-1)*dx;
y(i,j) = (j-1)*dy;
end
end
for j=1:ny
for i=1:nx
if (x(i,j) >= 0.5 && y(i,j) >= 0.5)
p(i,j) = 0.4;
r(i,j) = 0.5313;
u(i,j) = 0.0;
v(i,j) = 0.0;
elseif (x(i,j) < 0.5 && y(i,j) >= 0.5)
p(i,j) = 1.0;
r(i,j) = 1.0;
u(i,j) = 0.7276;
v(i,j) = 0.0;
elseif (x(i,j) < 0.5 && y(i,j) < 0.5)
p(i,j) = 1.0;
r(i,j) = 0.8;
u(i,j) = 0.0;
v(i,j) = 0.0;
elseif (x(i,j) >= 0.5 && y(i,j) < 0.5)
p(i,j) = 1.0;
r(i,j) = 1.0;
u(i,j) = 0.0;
v(i,j) = 0.7276;
end
c(i,j) = sqrt((gamma*p(i,j))/r(i,j));
end
end
Eig1 = abs(u) + c;
Eig2 = abs(v) + c;
dt = CFL*dx./max(Eig1(:),Eig2(:));
nt = floor(tMax/dt);
for k=1:nt
for j=1:ny
for i=1:nx
E(i,j) = p(i,j)./(gamma-1) + (0.5*r(i,j))*(u(i,j).^2 + v(i,j).^2);
Q(i,j,1) = r(i,j);
Q(i,j,2) = r(i,j).*u(i,j);
Q(i,j,3) = r(i,j).*v(i,j);
Q(i,j,4) = E(i,j);
F(i,j,1) = r(i,j).*u(i,j);
F(i,j,2) = r(i,j).*u(i,j).^2 + p(i,j);
F(i,j,3) = r(i,j).*u(i,j).*v(i,j);
F(i,j,4) = u(i,j).*(E(i,j) + p(i,j));
G(i,j,1) = r(i,j).*v(i,j);
G(i,j,2) = r(i,j).*v(i,j).*u(i,j);
G(i,j,3) = r(i,j).*v(i,j).^2 + p(i,j);
G(i,j,4) = v(i,j).*(E(i,j) + p(i,j));
end
end
for j=1:ny-1
for i=1:nx-1
ah1(i,j) = max(abs(u(i,j)) + c(i,j), abs(u(i+1,j)) + c(i+1,j));
ah2(i,j) = max(abs(v(i,j)) + c(i,j), abs(v(i,j+1)) + c(i,j+1));
Fh(i,j,:) = 0.5*(F(i+1,j,:) + F(i,j,:) - ah1(i,j).*(Q(i+1,j,:) - Q(i,j,:)));
Gh(i,j,:) = 0.5*(G(i,j,:) + G(i,j+1,:) - ah2(i,j).*(Q(i,j+1,:) - Q(i,j,:)));
end
end
Qnew(:,1,:) = Qnew(:,2,:);
Qnew(1,:,:) = Qnew(2,:,:);
Qnew(:,ny,:) = Qnew(:,ny-1,:);
Qnew(nx,:,:) = Qnew(nx-1,:,:);
for j=2:ny-1
for i=2:nx-1
Qnew(i,j,:) = Q(i,j,:) - (dt/dx)*(Fh(i,j,:) - Fh(i-1,j,:)) - (dt/dy)*(Gh(i,j,:) - Gh(i,j-1,:));
end
end
Q = Qnew;
r = Qnew(:,:,1);
u = Qnew(:,:,2)./Qnew(:,:,1);
v = Qnew(:,:,3)./Qnew(:,:,1);
E = Qnew(:,:,4);
p = (gamma-1)*(E - (0.5*Qnew(:,:,1))*(u.^2 + v.^2));
end
figure(1)
contour(x,y,r);
xlabel('x');
ylabel('y');
title('Density');
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
My idea is that the definition of the CFL in multidimensional cases is more complex. I give you a very simple example. If in the 1D scalar equation df+udf/dt=0 we introduce the cfl =u*dt/dx, it is quite straightforward considering that in the 2D counterpart df+udf/dt+vdf/dy=0 we have also the v*dt/dy component of the cfl.
Now the real issue is in how they affect the numerical stability. But for giving an answer you should always consider the numerical method. For example, if you use a forward time and first order upwind then you get into the condition: u*dt/dx + v*dt/dy<=1 If you use different methods you can get different stability conditions. In the case of non-linear equations the problem is much more difficult, the linear stability analysis gives some approximate indications but you have to consider that u and v are local (as well as the sound velocity). In general, I suggest to compute dt from the worst conditions you can consider in you flow problem. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 10  |
Hi FM Denaro,
I agree with your suggestion. With that being said from literature it seems that you calculate your time step from the system's largest eigenvalue. As such I have tried implementing that along with playing around with numbers, but have reached no luck. In fact, I am getting "NaNs" in my arrays, which I know is from the CFL condition not being satisfied (that I know of). Would maybe trying RK3 or RK4 help with the time step restrictions? |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
First, I suggest to try entering into the stability region by diminuishing progressively the time step. If that does not work it is likely you have a bug in the code. |
||
|
|

|
||
|
|
|
#5 |
|
New Member
Join Date: Aug 2016
Posts: 1
Rep Power: 0  |
Higher CFL number means higher time step limit.But to be able to use a larger CFL number,method should be more stable which means number of step should be higher. NAN solution comes probably because of using time in the unstable region. Try to increase number of step, i.e. use RK4 instead RK2. In addition, use lower CFL number. About the calculation of time step from CFL number, it will not be that easy for 2D case. I can recommend you to look at Computational Gasdynamics, Culbert B. Laney or Computational Fluid Dynamics for Engineers, Klaus Hoffmann and Steve T.Chiang
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
You may want to consult Blazek, Computational Fluid Dynamics, 3rd ed., paragraph 6.1.4 (pp. 173) for an account of possible methods to determine the stability time step. For cell centered finite volume on unstructured grids i currently use:
dt_c = CFL * V_c / SUM_f_c[(conv_f+visc_f)*A_f] where V_c is the volume of cell c, the SUM_f_c is over the faces f of cell c, A_f is the face area and conv/visc_f are the maximum (in value) eigenvalues of the convective and viscous contributions. In your case the viscous one is null but, for the convective one, i would use: conv_f = ABS(u_j n_j) + c where n_j is the j-th component of the face normal and u_j is the j-th component of the face velocity. Maximum allowable CFL is obviously scheme dependent. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 10  |
Hi everyone,
I greatly appreciate all the helpful replies, however I was able to detect the issue in the code. I needed to have (r0, u0, v0, E0) and use that to get (r, u, v, E). In fact, my CFL condition I had is currently working good. That being said I have a side question: Since I am using the TVD Lax Friedrichs (aka Rusanov aka Local Lax Friedrichs) would implementing the TVD Runge Kutat (3rd order) make a significant improvment in terms of the accuracy? I am currently writing a hydrodynamics code for computing fluid instabilities, such as Rayleigh-Taylor instability and Kelvin Helmholtz instability. |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
Well, you can get an improving in the temporal accuracy but the leading term of the local truncation error will be always constrained by the spatial discretization of the L-F method. |
||
|
|

|
||
|
|
|
#9 |
|
New Member
Animesh Bhowmik
Join Date: May 2018
Posts: 3
Rep Power: 7  |
Quote:
Can u provide the link of the reference paper/journal in which the detailed discussion on 2D Local Lax Fedrich method is explained |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 10  |
Instead of a 1D integral of the flux you are dealing with a 2D surface integral. Since for a 2D conservation law you have 2 fluxes, say F and G (assuming you have no source terms) you need to apply the flux discretization to both at the faces of your control volume. A good reference is the book by Toro or Leveque. If you are an engineer you may appreciate the book by Toro more. Mind you, this was my first 2D code as I was just starting to learn CFD, so I think there are errors.
|
|
|
|

|
|
|
|
|
#11 | |
|
New Member
Truong Dang
Join Date: Oct 2016
Location: Vietnam
Posts: 21
Rep Power: 9  |
Quote:
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Suitable inlet boundary condition for a compressible flow simulation | siw | FLUENT | 13 | October 9, 2018 23:54 |
| Smallest element, simpleFoam and CFL condition | jbernardo | OpenFOAM | 10 | September 27, 2017 11:50 |
| outlet boundary condition for compressible flow with no definite details | chem engineer | FLUENT | 2 | July 12, 2015 19:51 |
| Analytic solution for 2D steady Euler equations | jojo81 | Main CFD Forum | 0 | October 15, 2012 12:05 |
| Euler equations? | Jan Ramboer | Main CFD Forum | 2 | August 19, 1999 01:58 |