 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
The generally reported theory of von Neumann is focused on the evolution of the round-off error, that is a finite dimensional vector that is superimposed to the numerical solution of the discrete equation, assumed in absence of a finite precision arithmetic.
That is the discrete equation is Ad ud=0 And the round-off error is the vector e=ud-uro When the discrete operator is applied to e we exploit Ad ud=0 but in literature is generally reported (see Hirsch or Anderson) that also Aduro=0, therefore the equation to study for the stability constraints is Ad e=0 1) Why is it assumed that the RHS vanishes? I found no theoretical reasons to assume Aduro=0. 2) When the round-off error is introduced should'nt be considered its action also on the discrete operator Ad, that is Ae=Ad-Aro ? |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
|
This is a good question and I dont have a good answer.
Suppose you have a time update scheme 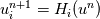 for which you have shown stability 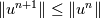 under some time step condition. In actual computation we get 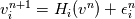 where each 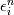 is of the order of is of the order of 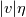 where where 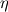 is the unit round of the computer. So we get an estimate of the form is the unit round of the computer. So we get an estimate of the form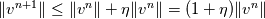 and the solution norm might increase by a fraction 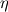 in one time step. in one time step.But this is a coarse argument and it ignores the fact that roundoff errors also cancel one another. Maybe if you use probabilistic arguments to account for the distribution of roundoff errors, you get a more precise estimate. These things would have been studied in the past but I dont know any good literature. What we are told in class is that if your method is fourier stable, and you use enough precision, then you dont have to worry about roundoff error in most applications. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
At the best of my knowledge, the literature does not clarify the issue.
The original papers von Neumann, J., Richtmyer, R.D. (1947), "On the Numerical Solution of Partial Differential Equations of Parabolic Type", LA Report 657, Crank, J.; Nicolson, P. (1947), "A Practical Method for Numerical Evaluation of Solutions of Partial Differential Equations of Heat Conduction Type", Proc. Camb. Phil. Soc., 43: 50-67, doi:10.1007/BF02127704 Charney, J. G.; Fjørtoft, R.; von Neumann, J. (1950), "Numerical Integration of the Barotropic Vorticity Equation", Tellus, 2: 237-254, doi:10.1111/j.2153-3490.1950.tb00336.x as well as the books of Hirsch and Anderson, simply stated that the discrete equation for the evolution of the round-off error has the RHS set to zero, that is exactly corresponds to the solved discrete equations. This is explained simply stating that both Adud=0 and Aduro=0. But there is no further argumentation to assess the latter is really satisfied in a finite precision. I mean, the latter is the equation that is not really solved in a computer program as Ad is the operator not affected by the round-off. I think that using Maple in symbolic calculus that can be shown. I could also change my question in: If I would able to do the computation by hand (or without introducing the finite precision responsible of the round-off), there is no more concerns about numerical stability, isn't that? |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Jul 2009
Posts: 351
Rep Power: 18  |
What I always understood (following Hirsch's description) is that the operator is linear, and the actual output of the system can be written as the sum of two functions - one of those is the exact solution to the difference equation and the other is an error term. Each piece equals zero identically because the operator is linear. As far as I know, that's the only justification. So it's not a flaw as much as a limitation to linear systems. The results are then extended to non-linear systems on an ad-hoc basis. At least that's the way I was taught Von Neumann stability theory.
|
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
Linear assumption means only that the round-off errors sums to the numerical solution to provide the real vector of the solution at finite precision. Why this round-off affected solution is an exact solution of the discrete (and linear) operator that satisfies Adud=0. What we should assumed true is that also the the discrete operator is affected by the round-off error to provide Aro uro = 0. But that does not change the fact that Adero seems to me to be not zero as assumed by the von Neumann theory. I know that Anderson and Hirsch assumes such identity for the equation that describes the evolution of the round-off error but I did not find a theoretical basis. |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Join Date: Jul 2009
Posts: 351
Rep Power: 18  |
If you are suggesting that the operator itself needs to be examined for its effect on stabilty, then I'm not sure that Von Neumann analysis is suitable. The VN error analysis is founded on the idea that the operator is linear, and so any sum of solutions will equal a third solution. It sounds like you are suggesting the need for a non-linear stability analysis. But I may not be understanding what you are saying.
|
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
The problem is that Ad is the exact discrete operator we write by hand on a paper at infinite precision. And the solution that satisfies Ad ud = 0 is assumed at exact precision, too. If we sum (linear assumption) to the solution ud a vector of the round-off error to express uro = ud + ero when you apply this operator to both sides we have only the constraint that ud satisfies exactly the equation. I dont know how to figure it out a theoretical assessment that ensures also Aduro=0 to get the common homogeneous equation for the error. You can always start by considering the real finite precision computation as the equation Aro uro =0 Thus (Ad + Ero )(ud + ero )=0 The problem is still due to the fact that we do not recover the von Neumann equation Ad ero =0 but the RHS has a source term affecting the evolution of the round-off error. |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
I have not found anything else in literature addressing this issue, I will try to do some numerical check in matlab
|
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
After further reading, I finally think that some conclusions can be driven :
1) starting from the original von Neumann theory (1947), considering what stated also in the book of Trefethen (https://people.maths.ox.ac.uk/trefethen/4all.pdf), the analysis considers only the amplification factor of the numerical scheme, round-off is never explicitly considered in the original idea. 2) we could argue why some textbooks (for example Hirsch) illustrated the theory on the basis of the round-off error evolution. 3) According to the statement of Trefethen, the stability could be analysed by means of the discretization error, too. However, the discrete equation for the evolution of such error is not homogenous, a fact that changes the evaluation of the analysis. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
For interested readers, I wrote a note for eduational purpose
https://www.researchgate.net/publica...eory_revisited |
|
|
|

|
|
|
|
|
#11 | |
|
Senior Member
Kira
Join Date: Nov 2020
Location: Canada
Posts: 435
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
|
Quote:
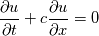 on a unform grid with nodes 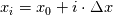 with with 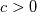 , which leads to the following scheme: , which leads to the following scheme: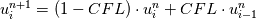 where 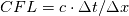 . Now, if you take an initial condition (time level n) which is 0 everywhere except, say, in nodes 2 and 3, where it is 1, then at the next time step (time level n+1) you have: . Now, if you take an initial condition (time level n) which is 0 everywhere except, say, in nodes 2 and 3, where it is 1, then at the next time step (time level n+1) you have: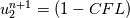 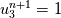 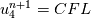 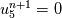 Take 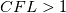 and you have problems, but I don't think I made any roundoff errors at all. Do I miss something in the reasoning? I think it is interesting to also note that node 5 won't get anything at all, no matter how high the CFL. and you have problems, but I don't think I made any roundoff errors at all. Do I miss something in the reasoning? I think it is interesting to also note that node 5 won't get anything at all, no matter how high the CFL.
|
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
Paolo, you are right but you know that it is quite common to present the numerical stability analysis while introducing the concept of "evolution of the error", "amplification factor of the error", and so on, using such statements while referring to finite numerics. In my note I followed the literature and I still don't know why the original paper of von Neumann was then, somehow, misunderstood. In his original paper the stability analysis is performed on the basis of the discrete equation for the resolved variable, no error equation is introduced. And I don't know why the error equation was then introduced by some authors in a wrong form, that is as homogeneous equation. Admittedly, I used to teach to the student the stability analysis following the CFD textbooks and the evolution equation for the error but I think that if we really want to analyze the topic in a modern a rigorous way, it is now time to consider the correct equations for bot the discrete and the continous errors. |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
I strongly suggest to read the original von Neumann's paper...
|
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
|
The way I see the matter on the stability is that once you pick up a stencil, a grid and a time step, then:
|
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
|
Quote:
 Jokes apart, I've read your note (but not the original papers you mention), and I also remember the stability often being referred with respect to roundoff errors. |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Are you able to download that paper? I can send you if you aren’t
|
|
|
|

|
|
|
|
|
#18 | |
|
Senior Member
|
Quote:
Returning to the issue, one can also see that, for the specific scheme I picked up, it turns out that every node will always contribute, at the next time step, a fraction 1-CFL of its value to the same node and a fraction CFL to the one next to it along the flow, no matter what. So, in a way, stability is a sort of conservation statement for the stencil in use. |
||
|
|

|
||
|
|
|
#19 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
but you need to generalize the analysis also for parabolic equations... I send you the paper |
||
|
|

|
||
|
|
|
#20 | |
|
Senior Member
|
Quote:
For purely explorative reasons, one could devise a scheme where first each node, according to the local characteristic speed, marks all the nodes within its region of influence and then each node evolves using a stencil with al the nodes that marked it in the first step... still, it is unclear how such stencil weights should be constructed |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Von Neumann Stability | mathgra | Main CFD Forum | 1 | July 2, 2018 09:57 |
| Why we use finite number of Terms in Fourier Decomposition of Error in Von Neumann St | alibaig1991 | Main CFD Forum | 2 | January 26, 2018 14:46 |
| stress analysis -Von Mises Theory | watashiwa | OpenFOAM | 7 | October 15, 2010 15:43 |
| Lax method stability via von neumann analysis | morteza08 | Main CFD Forum | 1 | June 5, 2010 12:43 |
| wmake compiling Problem with OF1.5 | openTom | OpenFOAM Installation | 4 | May 3, 2009 14:44 |