
 |
Quote:
If you consider the internal energy equation, that is the temperature equation, you see the same concept you wrote above in terms of closure expressed by means of a Fourier-like turbulent heat flux. However, while in case of a passive temperature that can be somehow justified, in case of a coupling to the other variables, there are further considerations. That issue is analysed in a couple of papers by Lilly. |
There is a tendency to do everything for velocity because we are explicitly invoking the eddy viscosity hypothesis, which is a pretty big theoretical leap.
You still need to write down the turbulent flux of other scalars at some point, which you don't have to obtain these by Reynolds analogy. But I would write down the velocity one first (put it at the top of the page so to say) just so it is clear the eddy viscosity hypothesis is the one being used. I would not for example, write down the turbulent flux for an arbitrary scalar and pretend like I have a magic wand that can always prescribe the right turbulent diffusivity coefficient. |
Quote:
The "magic wand" fallacy you spoke of is something I worry about very much. In the end, I realized that working out the turbulent fluxes in general isn't as useful as I first thought, and caused my discussion to lose focus and formalism very quickly. In that sense I could just stick with a relevant scalar variable (i.e., velocity component) and maintain a more concrete formulation. It is also one of those things where if you can do this for velocity, you can transfer the principle to other scalar variables. Thanks, Gerry. |
Here's the thing.
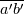 is pretty much the cross-correlation between a and b (for real a and b, it is the cross-correlation). To suggest that the cross-correlation between two arbitrary random variables can be re-written as a scalar times the gradient of is pretty much the cross-correlation between a and b (for real a and b, it is the cross-correlation). To suggest that the cross-correlation between two arbitrary random variables can be re-written as a scalar times the gradient of 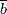 is pretty weird. If you told that someone not in the know, they'd either tell you that you're just wrong or give you really funny looks. is pretty weird. If you told that someone not in the know, they'd either tell you that you're just wrong or give you really funny looks.Context and justification are paramount in this case. It works because one of those things is u and because we apply the gradient-diffusion model. We are imposing these behavior rather than derive it. We shouldn't even be writing it with an equal sign, because it's not an equality. |
Quote:
|
There is a strong impact from the history for the present use of the eddy viscosity concept.
It could be also questionable the fact that a term coming from the hyperbolic part is modelled as a non-linear parabolic term. |
Quote:
On your second comment ... my first CFD code (from a long time ago) modelled the hyperbolic term with a parabolic treatment, although eddy viscosity was still an elliptic term. Ironic, isn't it? Gerry. |
Quote:
That is one of the questionable aspect of the eddy viscosity model, that is it changes the original mathematical character. That is due to the history and tradition of RANS approach. In LES there are modern SGS models where the original character is retained (dynamic similarity model, deconvolution model and so on). |
| All times are GMT -4. The time now is 09:31. |