Least approximation of derivative
 

Greetings,

Recently, I've read some papers in which they are using least-square to approximate the 2bd-order derivatives of a given 1-D data. I couldn't figure out how to do this, and I couldn't find any helpful references online.

Can anyone give me some hint, or recommend some references?

Appreciate it!


Edit: To be more specific, my purpose is to evaluate the following 2nd-order derivative



where is just the integer wavenumber, and is a given function in spectral space.

Are you referring to a cell-centered gradient approximation using a least-squares-based approach?

The general idea is that you write a 1st order taylor series approximation of a variable phi in the neighborhood n of the point c where you need the gradient (it is used for gradients in general) and assume that:

phi_n = phi_c + dphi/dx_i * (x_n-x_c)_i

Write this for all the available neighbors of a given point c and you get a system of equations that, in most cases, needs to be solved by a least squares method because you have more neighbors than gradient components.

However, the exact least squares solution of the equations is available and you don't typically solve it by a numerical procedure.

There is abundant literature on this. I suggest the book by Blazek as textbook reference because it is the one that covers it best (he and Haselbacher actually developed one of the available closed solutions to the problem).

EDIT: a different version of the exact solution (basically, you have the one based on solving the normal equations and the one based on QR factorization) can also be found in several of the early works of Prof. Z. J. Wang but, unfortunately, each one of them has a slight little error, and you need to look at all of them together to catch it.

Let me also highlight that the work of Blazek and Haselbacher is more general and has, indeed, been extended to higher than first order approximations (used for k-exact rexonstructions) as well as to filters for unstructured grids.

Doru Caraeni also put forward some developments/derivations for the easy application for 3rd order codes

Finally, Nishikawa and coworkers have also made several studies recently

Or you simply use this slide:

edit: By the way it is called Least Squares!

https://i.ibb.co/B2qBQVZ/leastsquares.png

Maybe, but I am not sure. The paper I read is using this least-squares approximation to approximate the 2nd-order derivative of the energy flux of HIT in spectral space. The reason they're using this is because the underlying grid is non-uniform.

Is this applicable to 1D case? I am just looking for an approach to differentiate a function on a non-uniform grid. The paper I referred to use this least-squares approximation to find out the 2nd-derivative of a given dataset.

I did some digging after I posted this thread, most of the contents are applied to CFD (at least from what I can tell). However, I am looking for a general approach that can be simply applied to evaluate differentiations of a given 1D data with non-uniform grid; and that's it, I don't need fancy algorithms that can solve complex fluid problems. So I think my need is just a simple numerical analysis of 1-D derivative. Do you think the approach you mentioned can be used for this purpose?

Sure you can! In 1D with equidistant distributed data this will result in a standard 2nd order FD stencil. However you can use it also for non-equidistant data. For a second order derivative simply apply the operator twice.

I think you make the problem harder than it is. Note that



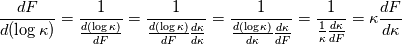and therefore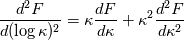

.

This is more easy to discretisize.

Regards

Nice point, but probably they have very different accuracy when discretized for typical energy spectra, say,
for a function of the form 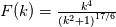, representative of the energy at large large scales (i.e., no dissipative range).

When you look at this in log k the peak is much more spread (besides the fact that the delta log(k) are much smaller than the delta k).

However, without knowing the original use case for least squares here, Ferziger & Peric has straighforward formulas for both 1st and 2nd derivatives in 1D for non uniform grids, without need to resort to anything fancy.

That's true. I think he has to test, which representation works better.

Thanks for your previous reply. So I'll probably try both approaches.

Could you explain more on this specific case that you gave? Why this spreading peak would affect the accuracy? Is it because it can't be accurately represented on a uniform grid?

Well, the function I used is just an example of how the energy spectra behave at low wave numbers (I used k^4, but k^2 would have been another possibility), where they tipically have a peak.

Now, what approach is more suited obviously depends from what the final goal is, but I would point out the following:

1) The formula with log k is just a second derivative, while the formula with k has two derivatives (first and second) multiplied by k and k^2 respectively. More work and typically more error.

2) The steps in k are much larger than those in log k, so this is necessarily linked to higher error

3) Now that I think more about it, this might simply be a restatement of 2 but, if you plot the function above as function of k and of log k, the latter is much more smoother around the peak, which means that any given formula would give less error.

When I wrote the message this morning, I actually tried both formulas and they indeed differ at low wavenumbers for the function I mentioned. I deleted the script I used, but I suggest you to make a similar test to better understand them both.

I see. Great explanation and thanks a lot!