 |
|
|
[Sponsors] | |||||
Point where Shear Stress is 10 Pascals based on sin Velocity Profile |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
I did a Civil Engineering course some years ago and from my textbook I had a question on this.
Q4 Annotation 2020-06-08 211656.png I have made an attempt at the calculations for this question based on the attached research below, but I am not getting the correct answer. Shear Stress Distance pg 1.png Shear Stress Distance pg 2.png Shear Stress Distance pg 3.png Shear Stress Distance pg 4.png Where it says Equating the values of τw from Eqs (2) and (3), we obtain τw = pi * μ * U / (2 * Boundary layer Thickness) where τw = Shear Stress = 10 Pascals, μ = viscosity = 0.0018 Ns/m^2 and U = 15 m/s Based on this 10 * 2 = (pi * 0.0018 * 15) / Boundary layer Thickness so Boundary layer Thickness = 0.00424 m I have then tried to find x (distance from leading edge) from the boundary layer thickness formula below. Boundary Layer Thickness = 4.79 * square root [(μ * x) / (ρ * U∞)] where μ = viscosity, ρ = Density and U∞ = Velocity Boundary Layer Thickness = 4.79 * square root [(0.0018 * x) / (1000 * 15)] 0.00424 = 4.79 * square root [((0.0018/9.81) * x) / (1000 * 15)] 0.00424 = 4.79 * square root [(0.0018/9.81) / (1000 * 15)] x^0.5 x^0.5 = 0.00424 / [ 4.79 * square root [(0.0018/9.81) / (1000 * 15)]] x = 0.00424^2 / [ 4.79^2 * [(0.0018/9.81) / (1000 * 15)]] x = 64.06 m (no way this is far too big and is not the 2.25 mm answer) May someone please explain to me what things I need to understand, so that I can work towards the answer and get a better understanding on this ? Last edited by Rob Wilk; June 10, 2020 at 09:07. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Troy Snyder
Join Date: Jul 2009
Location: Akron, OH
Posts: 219
Rep Power: 18  |
Quote:
Your analysis appears to be correct to me. Using your result for the wall shear stress, I get a location of x = 6.54 [m]. Note that in your calculation at the end, you seem to have the acceleration due to gravity floating around? Also, repeating the calculation using a parabolic velocity profile in the von Karman integral (to get an expression for wall shear) and using the Blasius expression for boundary layer thickness, I get a location x = 6.7 [m]. What textbook is this? Is there an errata? It appears that the numerical answer provided may not be correct. |
||
|
|

|
||
|
|
|
#3 | |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
Quote:
That formula τw = pi * μ * U / (2 * Boundary layer Thickness) is for when y = 0 and y is not always equal to 0. I think that I am meant to be calculating x, the distance along plate. So I just wonder if I should actually be using the other formula τw = 0.137 ρ * U^2 * d (that boundary layer symbol) / dx for working this out, because I think x needs to be calculated. If it is to be done that way, I wonder how you would rearrange d (that boundary layer symbol) / dx part of the equation, so that x can be solved. |
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Troy Snyder
Join Date: Jul 2009
Location: Akron, OH
Posts: 219
Rep Power: 18  |
Quote:
You have an expression for 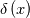 . See your last image of your original post. Take the derivative and substitute into the equation you derived for the wall shear. Then insert your known parameters and solve for x. . See your last image of your original post. Take the derivative and substitute into the equation you derived for the wall shear. Then insert your known parameters and solve for x.
|
||
|
|

|
||
|
|
|
#5 | |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
Quote:
I have tried to calculate this based on what you have said. Firstly I am finding an expression for boundary layer thickness Boundary Layer Thickness = 4.79 * sqrt (μ0 / (ρ * U0)) * x^1/2 Now we need to find the derivative for this boundary layer thickness formula So differentiate boundary layer thickness d (boundary layer thickness) / dx = 4.79 * sqrt (μ0 / (ρ * U0)) * 1/2 x^1/2 - 1 d (boundary layer thickness) / dx = 4.79 * sqrt (μ0 / (ρ * U0)) * 1/2 x^-1/2 d (boundary layer thickness) / dx = 4.79 * sqrt (μ0 / (ρ * U0)) * 1/2 / x^1/2 Now I will put d (boundary layer thickness) / dx into the shear stress formula We will use the following shear stress formula: τw = 0.137 ρ * U^2 * d (that boundary layer thickness) / dx τw = 0.137 ρ * U^2 * 4.79 * sqrt (μ0 / (ρ * U0)) * (1/2 / x^1/2) Now we can put in the values and solve for x τw = 0.137 * 1000 * 15^2 * 4.79 * sqrt (0.0018 / (1000 * 15)) * (1/2 / x^1/2) τw = 147651.75 * 0.00034641 * (1/2 / x^1/2) τw = 25.574 / x^1/2 The question has given Shear Stress τw = 10 Pa or 10 N/ m^2 so 10 = 25.574 / x^1/2 10 x^1/2 = 25.574 x^1/2 = 25.574/ 10 x^1/2 = 2.5574 x = 2.5574^2 = 6.54 m I am not there yet why is this, I believe I have done my differentiation correct with boundary layer thickness. How do you get this answer of 2.25 mm or is it not possible ? Last edited by Rob Wilk; June 15, 2020 at 23:22. |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Troy Snyder
Join Date: Jul 2009
Location: Akron, OH
Posts: 219
Rep Power: 18  |
Quote:
2.) I highly recommend that you manipulate/derive equations symbolically and only enter numerical values at the very end. This is far less error prone. Additionally, you are much more likely to solicit helpful responses on this forum if the expressions are presented symbolically. 3.) Regarding my previous post, I got the result x = 6.54 [m]. I did not get the numerical result provided in the text and question its validity. |
||
|
|

|
||
|
|
|
#7 | |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
Quote:
I have tried to calculate this based on what you have said. Firstly I am finding an expression for boundary layer thickness Boundary Layer Thickness = 4.79 * sqrt (μ0 / (ρ * U0)) * x^1/2 Now we need to find the derivative for this boundary layer thickness formula So differentiate boundary layer thickness d (boundary layer thickness) / dx = 4.79 * sqrt (μ0 / (ρ * U0)) * 1/2 x^1/2 - 1 d (boundary layer thickness) / dx = 4.79 * sqrt (μ0 / (ρ * U0)) * 1/2 x^-1/2 d (boundary layer thickness) / dx = 4.79 * sqrt (μ0 / (ρ * U0)) * 1/2 / x^1/2 Now I will put d (boundary layer thickness) / dx into the shear stress formula We will use the following shear stress formula: τw = 0.137 ρ * U^2 * d (that boundary layer thickness) / dx τw = 0.137 ρ * U^2 * 4.79 * sqrt (μ0 / (ρ * U0)) * (1/2 / x^1/2) Now we can put in the values and solve for x τw = 0.137 * 1000 * 15^2 * 4.79 * sqrt (0.0018 / (1000 * 15)) * (1/2 / x^1/2) τw = 147651.75 * 0.00034641 * (1/2 / x^1/2) τw = 51.148 / x^1/2 The question has given Shear Stress τw = 10 Pa or 10 N/ m^2 so 10 = 51.148 / x^1/2 10 x^1/2 = 51.148 x^1/2 = 51.148/ 10 x^1/2 = 5.1148 x = 5.1148^2 = 26.16 m Just wondering how you got x = 6.54 m, what formulas did you use for that ? It seems that answer of 2.25 mm is impossbile to get. |
||
|
|

|
||
|
|
|
#8 | |
|
Senior Member
Troy Snyder
Join Date: Jul 2009
Location: Akron, OH
Posts: 219
Rep Power: 18  |
Quote:
You made an error going from (1) to (2) below... (1) τw = 147651.75 * 0.00034641 * (1/2 / x^1/2) (2) τw = 51.148 / x^1/2 Again, I cannot emphasize enough to manipulate the equation symbolically and only insert numerical values at the very end. Your numerical mistake is a testament to how error-prone your evaluation of the answer is. |
||
|
|

|
||
 |
| Tags |
| boundary layer, shear stress equations |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Shear Stress Calculation in the flow. | auburnuser | FLOW-3D | 11 | May 12, 2018 13:49 |
| Plotting Shear Stress | michael.collins | STAR-CCM+ | 1 | January 21, 2016 11:39 |
| UDF for wall slipping | HFLUENT | Fluent UDF and Scheme Programming | 0 | April 27, 2011 12:03 |
| shear stress scalar definitions? | Novak Elliott | CFX | 0 | April 6, 2003 01:45 |
| What is the detail definition of wall shear stress | zjm | FLUENT | 0 | January 2, 2002 07:43 |