 |
|
|
[Sponsors] | |||||
Laminar Boundary Layer Thickness before Transition |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
I did a Civil Engineering course some years ago and from my textbook I had a question on this.
Chapter 14 - Question 3.png I have calculated boundary layer thickness based on the boundary layer velocity profile given, The Boundary Layer Thickness = sqrt 180 * [(μ0) / (ρ * Uo)]^1/2 * x critical^1/2 where μ0 = viscosity of water = 1.308 * 10^-3 kg/ ms ρ = density of water at 10 degrees C = 999.7 kg/ m^3 from google search and Uo = 5 m/ s first we have to find x critical (length of plate) at the critical point when it transitions from laminar to turbulent. We have been given the Transition Reynolds number = 4 * 10^5 Now Transition Reynolds Number = (ρ * Uo * x critical) / μ0 Transition Reynolds Number * μ0 = (ρ * Uo * x critical) x critical = (Transition Reynolds Number * μ0) / (ρ * Uo) x critical = (4 * 10^5 * 1.308 * 10^-3) / (999.7 * 5) x critical = 0.10467 m Boundary Layer Thickness = sqrt 180 * [(1.308 * 10^-3) / (999.7 * 5)]^1/2 * 0.10467^1/2 Boundary Layer Thickness = 2.22 mm The textbook answer is 0.906 mm Why is my answer out ? May someone please explain to me what things I need to understand, so that I can work towards the answer and get a better understanding on this ? Last edited by Rob Wilk; June 10, 2020 at 03:24. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 347
Rep Power: 10  |
Dear Rob:
I think the expression for laminar boundary thickness should be 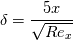 and the critical location, as you pointed out, can be found using the definition of Reynolds number: 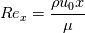 With  = 1000, the critical location is 0.10464 m, and the boundary layer thickness should be 0.827 mm. It's closer to the 0.906 mm provided by the textbook. = 1000, the critical location is 0.10464 m, and the boundary layer thickness should be 0.827 mm. It's closer to the 0.906 mm provided by the textbook.You might want to check what criterion is used for boundary layer thickness, the expression 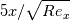 used here is known as the 99% criterion. To get the textbook solution it is more like 5.4, which might correspond to 99.999%. used here is known as the 99% criterion. To get the textbook solution it is more like 5.4, which might correspond to 99.999%.I also don't understand why the velocity profile was provided; perhaps there is a follow up question, in which it was used. Gerry. |
|
|
|

|
|
|
|
|
#3 |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
Quote:
I haven't had much time to look at this sort of stuff recently because I have been busy with other things. My thinking was that the velocity profile was provided, so that you can come up with the formula for boundary layer thickness. That was how I calculated it , but I didn't get the correct answer. It looks like you have calculated the same critical location as me. From what you have said, you think that Boundary Layer is close to (5.4 x) / (sqrt Rex), I'll go through the calcs to check that out. I just wonder how you arrive at that formula ? the 5.4 is quite different from the sqrt 180 I used in my calculation. 99% criterion is that in relation to the free stream velocity ? |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 347
Rep Power: 10  |
Dear Rob:
You can perhaps use the velocity profile to derive the boundary layer thickness, not unlike the method used in the train question (link here). But in that case you still need some kind of shear stress. The expression for the skin friction coefficient the laminar boundary layer: 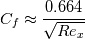 is, in fact, the result of the Blasius solution, which in effect makes the velocity profile superfluous, because the Blasius solution also comes with a velocity profile. The 5 you see is actually 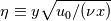 , a normalized vertical distance and, as you have pointed out, it is related to the freestream velocity. Since the Blasius vertical velocity profile is asymptotic, a commonly accepted criterion for finding , a normalized vertical distance and, as you have pointed out, it is related to the freestream velocity. Since the Blasius vertical velocity profile is asymptotic, a commonly accepted criterion for finding 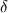 is to cut it off when is to cut it off when 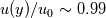 , the happens when , the happens when  . This should have been covered in most text books on fluid dynamics. . This should have been covered in most text books on fluid dynamics.So, it could be that the textbook author did not like this seemingly arbitrary cut-off, and wanted you to work out the boundary layer yourself. If you end up using the velocity profile to estimate the boundary layer thickness, the coefficient you get should in fact be closer to 5 (i.e., ~ 5.4 based on my calculations) than 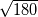 . .Gerry. Last edited by Gerry Kan; August 18, 2020 at 04:35. |
|
|
|

|
|
|
|
|
#5 | |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
Quote:
Using the formula which is similar to yours 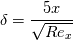 but in a different format. Putting these values μ0 = viscosity of water = 1.308 * 10^-3 kg/ ms ρ = density of water at 10 degrees C = 999.7 kg/ m^3 from google search and Uo = 5 m/ s into equation Boundary Layer Thickness = 0.906 mm = coefficient * [(1.308 * 10^-3) / (999.7 * 5)]^1/2 * 0.10467^1/2 and I get 5.474 So now its just a matter of working out how to get to that coefficient. You mentioned blassius, I'm not familiar with this 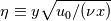 Just wondering if you don't mind are you able to please show how you would calculate to get to the coefficient ? This is the part of the question that I am not so sure about, once I get a good understanding on this I think it can get solved. Last edited by Rob Wilk; September 15, 2020 at 10:42. |
||
|
|

|
||
|
|
|
#6 | |
|
Member
Rob Wilkinson
Join Date: Apr 2020
Location: Wellington, New Zealand
Posts: 69
Rep Power: 5  |
Quote:
Just wondering if you got the chance to look into my previous reply It went like this I have worked out what coefficient will give the answer of 0.906 mm Using the formula which is similar to yours 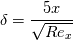 but in a different format. Putting these values μ0 = viscosity of water = 1.308 * 10^-3 kg/ ms ρ = density of water at 10 degrees C = 999.7 kg/ m^3 from google search and Uo = 5 m/ s into equation Boundary Layer Thickness = 0.906 mm = coefficient * [(1.308 * 10^-3) / (999.7 * 5)]^1/2 * 0.10467^1/2 and I get 5.474 So now its just a matter of working out how to get to that coefficient. You mentioned blassius, I'm not familiar with this 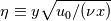 Just wondering if you don't mind are you able to please show how you would calculate to get to the coefficient ? This is the part of the question that I am not so sure about, once I get a good understanding on this I think it can get solved. |
||
|
|

|
||
 |
| Tags |
| boundary layer |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| y+ = 1 boundary layer mesh with snappyHexMesh | Arzed23 | OpenFOAM Running, Solving & CFD | 6 | November 23, 2022 15:15 |
| [snappyHexMesh] Help with Snappy: no layers growing | GianF | OpenFOAM Meshing & Mesh Conversion | 2 | September 23, 2020 08:26 |
| Question about adaptive timestepping | Guille1811 | CFX | 25 | November 12, 2017 17:38 |
| Error - Solar absorber - Solar Thermal Radiation | MichaelK | CFX | 12 | September 1, 2016 05:15 |
| Basic Nozzle-Expander Design | karmavatar | CFX | 20 | March 20, 2016 08:44 |