
 |
Quote:
Paolo, not in my field of personal work experience, I suppose you already checked Leveque and Hirsch, right? I can suggest also this review https://www.sciencedirect.com/scienc...050?via%3Dihub maybe some check to the textbook "Chung T.J. Computational fluid dynamics (CUP, 2002)" could be worthwhile. |
Quote:
The only papers I ever found on the subject are those I mentioned (and their direct descendant/parents from the same authors), and they don't mention anything or don't use Roe averages in the Fluent case. Every other paper I found (even books) just acritically copy that material. In the end, as I said, this is not, nor has ever been, a real issue per se, but I'm now starting to feel uncomfortable without certain pieces of information. |
Quote:
Have you checked also in the report "Building your own shock tube" by J. Naber? The primitive variables are used there. |
Just an update.
In the end, I decided that the EOS is not, by itself, ambiguous on how certain properties should be calculated, no matter what. In particular, in no occasion should I compute any thermodynamic quantity starting from anything different than the independent variables. Thus, as my independent variables are 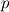 and and  , for the ideal gas EOS it means that, for example: , for the ideal gas EOS it means that, for example: is the only correct way to compute the density derivative with respect to pressure; that is, density can't appear in it (i.e., I can't use  ). ).Will see if this turns out problematic, but for the moment I feel it is the only reasonable approach. If something different is needed for the Roe scheme, than this must be handled outside the EOS routine, no matter how bad it looks. Still, with respect to a classical Roe scheme, this should only affect how the speed of sound is computed in the intermediate state. |
Dear Paolo,
the exact Riemann solver for the linearized hyperbolic system, more precisely the Roe solver for the Euler equations with general EoS, is not straight forward. With general EoS i refer to non-calorically perfect EoS, this includes e.g. ideal gases, real EoS or multi-component systems. The caloric perfect EoS case is a lucky accident: In general it is not possible to fulfill thermodynamic consistency and all three Roe properties (i) hyperbolicity, (ii) consistency, (iii) conservation, simultaneously. That makes total sense, since (as the name suggests) you are playing with mean values using the Roe averages. Simply spoken, thermodynamic laws are generally not applicable on averages. A neccecary condition to be fullfilled is, see e.g. Guardone and Quartapelle:  Summarizing: You have to define new reasonable conditions for the new unknowns, especially for the last Roe property. Original Roe: Roe Approximation of original Roe: Pike First multi-component Roe: Abgrall First real EoS Roe: Glaister Ideas of Larrouturou for multi-component systems: Larrouturou Other generalizations of Roe method: Liou Cox Toumi Vinokur Guardone Mottura Regards |
Again, no direct experience about that issue but the LES field of compressible flows has to do with the local averaging of the EOS. Is that approach valid?
|
I am no expert for compressible LES, especially for non-calorically perfect EoS. However, let me explain the problem you are facing with general EoS. The onedimensional Euler equations are given as
![\begin{pmatrix}
\rho \\
\rho u \\
\rho e
\end{pmatrix}_t +\begin{pmatrix}
\rho u \\
p + \rho u^2 \\
[ \rho e +p ] u
\end{pmatrix}_x = 0 \begin{pmatrix}
\rho \\
\rho u \\
\rho e
\end{pmatrix}_t +\begin{pmatrix}
\rho u \\
p + \rho u^2 \\
[ \rho e +p ] u
\end{pmatrix}_x = 0](/Forums/vbLatex/img/aea41332496ab29d30851efb7abed0f9-1.gif) . .Moreover, we have to keep in mind that an arbitrary caloric EoS (also called incomplete EOS) is needed to close the system  . Now we define the closed system as: . Now we define the closed system as:![\underbrace{\begin{pmatrix}
\rho \\
\rho u \\
\rho e
\end{pmatrix}_t +\begin{pmatrix}
\rho u \\
p+ \rho u^2 \\
[ \rho e +p ] u
\end{pmatrix}_x = 0 , \quad p=p(\rho,\epsilon) }_{:=\text{PDE}} \underbrace{\begin{pmatrix}
\rho \\
\rho u \\
\rho e
\end{pmatrix}_t +\begin{pmatrix}
\rho u \\
p+ \rho u^2 \\
[ \rho e +p ] u
\end{pmatrix}_x = 0 , \quad p=p(\rho,\epsilon) }_{:=\text{PDE}}](/Forums/vbLatex/img/42c7d3c6ccc206c4f81bfc5e926108c8-1.gif) . .Considering a Riemann problem (RP) with arbitrary constant values left and right: Situation A: A unique caloric perfect EoS, e.g.   Situation B: Spatial varying  , e.g. left , e.g. left  , right , right   Since the EoS is part of your equation system, you now challenge the problem of solving a RP for two different closed PDEs. As a byproduct, you are facing the problem of so called spurious pressure and velocity ocillations. Regards |
Quote:
I think that the problems should be better clarified between cell-averaged variables and pointwise fluxes. You do not write the differential form on the pointwise variables but on the cell-averaged variables. I have no great experience but I think that the PDEs are the issues, you need to write them as non-closed PDEs. |
Quote:
So, if I understand correctly, even just pretending that a certain average reduces to the Roe one when applied to non ideal gases is not, indeed, as easy as it may sound? Even if I don't care at all of what happens in the other non ideal cases? @Filippo, at the present state I only care about 1st order, constant states in left and right cells for a given face in 1D. Actually, if we look at this from the FD perspective, we don't even need the average concept, I think. I would just like that in the most relevant compressible case I'm going to handle I will correctly upwind the correct Riemann invariants. |
Quote:
Paolo, let us think first to the continuous set of equations, including the EOS. You know that the concept of the Riemann problem makes sense in a more different way, the differential form of the equations (you wouyld use in the FD manner) governs the variables that are averaged, see Eq.(4.9) in the textbook of Leveque. The fact that you use a first order discretization fro the flux reconstruction does not change the initial formulation of conservation laws. I think that one should first describe the mathematical problem in terms of cella-averaged values, pointwise flux, pointwise and averaged EOS and then introduce the discretization. Is maybe that issue generating confusion? |
Just for your interest, this is what I have so far in my scheme for the dissipation part
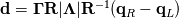 (but note that I don't use it in this form, I still use matrix products to avoid loosing control): (but note that I don't use it in this form, I still use matrix products to avoid loosing control):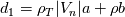 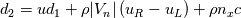 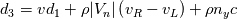 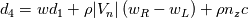 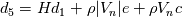 with: 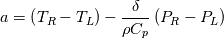 ![b = \frac{\theta_2}{2\rho s_2V_r^2}\left(P_R-P_L\right)+\frac{\theta_3}{2s_2V_r^2}\left[\mathbf{n} \cdot \left(\mathbf{V}_R-\mathbf{V}_L\right)\right] b = \frac{\theta_2}{2\rho s_2V_r^2}\left(P_R-P_L\right)+\frac{\theta_3}{2s_2V_r^2}\left[\mathbf{n} \cdot \left(\mathbf{V}_R-\mathbf{V}_L\right)\right]](/Forums/vbLatex/img/17d50208627c65b28265f1d782144821-1.gif) ![c = \frac{\theta_1}{2 \rho s_2} \left(P_R-P_L\right) +\left(\frac{\theta_2}{2 s_2} -|V_n| \right) \left[\mathbf{n} \cdot \left(\mathbf{V}_R-\mathbf{V}_L\right)\right] c = \frac{\theta_1}{2 \rho s_2} \left(P_R-P_L\right) +\left(\frac{\theta_2}{2 s_2} -|V_n| \right) \left[\mathbf{n} \cdot \left(\mathbf{V}_R-\mathbf{V}_L\right)\right]](/Forums/vbLatex/img/3d1f5bd7597a1ff7614e1f741dc4d77c-1.gif) 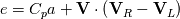 and: 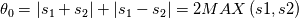 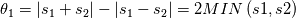 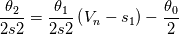 ![\frac{\theta_3}{2s2} = \frac{\theta_1}{2s2}\left[\left(V_n-s_1\right)^2+s_2^2\right]-\left(V_n-s_1\right)\theta_0 \frac{\theta_3}{2s2} = \frac{\theta_1}{2s2}\left[\left(V_n-s_1\right)^2+s_2^2\right]-\left(V_n-s_1\right)\theta_0](/Forums/vbLatex/img/28cd0e0b6acf339dd05021c6b0ca456a-1.gif) 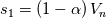 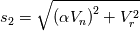 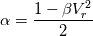 where 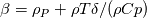 is the inverse of the speed of sound squared, is the inverse of the speed of sound squared, 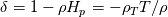 and anything without the R/L subscript to be evaluated at the Roe average. One could actually further simplify things by nothing that: and anything without the R/L subscript to be evaluated at the Roe average. One could actually further simplify things by nothing that: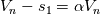 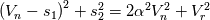 but I've found difficulties in proceeding further toward a version which could even remotely resemble the Roe one (not sure if it is also due to the certainly different eigenvectors I'm using). |
Quote:
|
Quote:
However, I can only speak from my own experience. The step towards non-caloric EoS is not as easy as it seems. You will encounter problems that you did not realize existed in the first place. |
If you are more interested in the Riemann problem theory for real materials i can suggest:
Menikoff and Plohr One of my favorite papers so far. Regards |
Another doubt I have regards the unsteady term for the preconditioned system when preconditioning is actually turned off.
As I wrote, for the preconditooned case one usually solves for: ![\mathbf{\Gamma}\frac{\partial \mathbf{q}}{\partial \tau} + \mathbf{\Gamma}\left[\mathbf{\Gamma}^{-1} \left(\mathbf{AM}\right)\right]\frac{\partial \mathbf{q}}{\partial x} = 0 \mathbf{\Gamma}\frac{\partial \mathbf{q}}{\partial \tau} + \mathbf{\Gamma}\left[\mathbf{\Gamma}^{-1} \left(\mathbf{AM}\right)\right]\frac{\partial \mathbf{q}}{\partial x} = 0](/Forums/vbLatex/img/a2601eaa3a0e0f6641533461dc66aef7-1.gif) where time really has to be interpreted as pseudo-time and the equations are correct only at steady state. Now with preconditioning "turned off" one would end up with: ![\mathbf{M}\frac{\partial \mathbf{q}}{\partial t} + \mathbf{M}\left[\mathbf{M}^{-1} \left(\mathbf{AM}\right)\right]\frac{\partial \mathbf{q}}{\partial x} = 0 \mathbf{M}\frac{\partial \mathbf{q}}{\partial t} + \mathbf{M}\left[\mathbf{M}^{-1} \left(\mathbf{AM}\right)\right]\frac{\partial \mathbf{q}}{\partial x} = 0](/Forums/vbLatex/img/b024f30b7f6983275c02997e07b2a74d-1.gif) where  and  The question then is, from the continuous point of view, as now we use  (instead of its preconditioning altered version (instead of its preconditioning altered version  ), is this now time accurate? If it is so, imagine the following discretization of the unsteady term: ), is this now time accurate? If it is so, imagine the following discretization of the unsteady term: If it is time accurate, does it mean that the following is correct?  I'm not sure that this actually holds at all. EDIT: Just to give context, the relevance of this comes from the fact that, if all of this holds, and one uses primitive variables, then one can completely avoid conservative variables also for the unsteady cases. EDIT2: Apparently, someone even made a paper on this kind of obviou possibility (https://research-information.bris.ac...ne.0195494.pdf). Yet, besides the journal quality, they seem too naive to be trusted. EDIT3: While the above is certainly true at the continuous level, I think it is also certainly false that it holds discretely (just as for the Roe average) for anything non linear. If indeed one consider the NS equations with an ideal gas and the backward Euler discretization of the density time derivative, what one obtains is:  which is generally different from the actual difference in density as computed at the two times:  So the question is, is this at least second order accurate in time? I think that one can show that this is indeed the case for the ideal gas by nothing that:  but I'm unsure on how to prove this in general (nor I actually tested all the remaining terms of the NSE) EDIT 4: Apparently, for the given 1st order backward Euler case with the idal gas EOS, all the terms are indeed exact within a 2nd order error term, except the kinetic energy contribution to the total energy, which also has a first order error of the form:  |
Roe average should (most likely!) not be used. Simple arithmetic average should be used from our experience and also as per Weiss, 1995 work where it is clearly stated
"Roe-averaged values are not used with preconditioning" https://arc.aiaa.org/doi/abs/10.2514...rnalCode=aiaaj |
Quote:
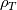 , and only that, needs to be computed as: , and only that, needs to be computed as: using the Roe density... still don't know why. So I had to use an ugly hack just for that:  |
Quote:
if you are talking about d rho / dP for construction of linear system to solve pressure correction then upwinded values of d rho / dP work just fine (I have n't looked into code for 2 years so bit vague here). Same should be okay for drho/dT I believe. For compressible flow I do not remember to do any hack and everything works just fine (Other than the upwinded values when needed). |
Quote:
1) rho, u, v, w, p, T and H are taken as classical roe averages 2) All the derivatives, except drho/dT, are computed from primitive variables only (i.e., p and T) at the Roe state computed in 1 3) drho/dT is computed as in 2, but then needs to be multiplied by the ratio between rho computed in 1 and rho computed in 2 This, actually, is independent from the specific average used in 1, and also works if it is an arithmetic average. The very important step is 3, which means that drho/dT in the Roe state for an ideal gas must be computed as -rho_ROE/T_ROE. Nothing of this seems relevant if you work with conservative variables in ideal gas cases, where you can just use the straightforward Roe receipt. Note that this receipt can solve, for example, the following shock tube case:  , ,  , ,  ; ;  , ,  , ,  which I couldn't solve with any other combination (the only thing I haven't tried yet is using step 1 for all the variables). All of this might or not have something to do with my specific eigenvectors, but I have no idea at the moment. |
| All times are GMT -4. The time now is 01:15. |