 |
|
|
[Sponsors] | |||||
Pi-Buckingham theorem and modified Froude number |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Rodrigo Villarreal
Join Date: Nov 2016
Posts: 25
Rep Power: 9  |
I've obtained the Reynolds number applying Pi-Buckingham theorem in my fluid dynamics course. It is indeed a powerful method for dimensional analysis, but it requires that all the main variables that affect the system must be independent of each other.
Does the modified Froude number can be obtained using this method even if the density of each phase is the same physical dimension? The definition of modified Froude number I'm analyzing is 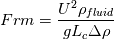 Thanks for your response. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,674
Rep Power: 65    |
Buckingham Pi theorem does not require all the parameters to be dimensionally independently. The Pi theorem is a statement that the dimensionally dependent quantities are relatable to a smaller set of dimensionally independent quantities. In Froude number for example, the length appears in multiple (actually all) variables: velocity, density, gravitational acceleration, characteristic length, and density difference; they all contain the dimension of lengths. The utility of real value of the Pi theorem is it gives you a count for how many dimensionless groupings you need to fix your set of equations. That is, once you have identified all the physical dimensions in your problem, it tells you how many numbers you need. You have identified Reynolds number and Froude number, Pi theorem tells you how many more you need. For example, regardless of how many phases you have and how many densities you might have, I know naively that at worst I can identify an equal number of density ratios as a dimensionless grouping that relates all the densities together. Pi theorem might give you that you need fewer than these.
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Rodrigo Villarreal
Join Date: Nov 2016
Posts: 25
Rep Power: 9  |
Thanks for your answer.
Now I understand that dimensions aren't a constraint in the Pi-Buckingham method. This explanation gives me a significant glimpse of understanding how it works. |
|
|
|

|
|
 |
| Tags |
| fluid, physical meaning, physics, physics of fluids |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Green's theorem or divergence theorem? | Hermano | Main CFD Forum | 0 | November 30, 2011 16:11 |