
 |
How many boundary conditions do we need for the pressure?
Hello guys,
I am still somewhat new to CFD (just starting my masters degree) so please bear with me if my question is dumb. I am simulating fluid flow in a channel for an assignment. The aim of the assignment is to simulate 2 dimensional incompressible Poiseulle flow, moving from left to right. It is a very simple simulation. There are no obstacles and it is a simple rectangular domain. For the velocity, I enforce a velocity inlet condition at the inlet and a homogeneous Neumann condition at the outlet. I enforce a homogeneous Dirichlet condition (no-slip) at the top and bottom wall. This all makes sense to me as the INSE are second order in u . But, when I was looking over some example tutorial cases in OpenFOAM, I noticed that their simulations were enforcing a boundary condition for the pressure on both the inlet AND the outlet, and correspondingly, on both the bottom AND the top wall. They typically used a homogeneous Neumann condition on the top and the bottom wall, a homogeneous Neumann condition on the inlet, and a Dirichlet condition on the outlet. This does not make sense to me from a mathematical point of view, because the INSE are first order in p in both the x and y coordinate, so specifying boundary conditions at only, for example, the bottom and left wall should already be enough to fully specify the solution. I know that the INSE are invariant under constant pressure shifts p --> p+p0 which gives the system a little extra freedom. I also know that typically the pressure is simulated using the pressure Poisson equation, which is of course second order. But this is a consequence of the INSE, not a governing equation in its own right. I would appreciate some elucidation on this topic. Thanks. |
Thank you for the response. I am familiar with the traditional polygonal domain example. Allow me to be more precise.
Let 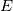 be a connected, open, bounded, convex subset of be a connected, open, bounded, convex subset of 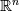 , where , where 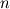 =2 or 3. (Think of some sort of ball.) Now draw a line through E. Because of the assumptions we made on =2 or 3. (Think of some sort of ball.) Now draw a line through E. Because of the assumptions we made on 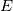 , this line intersects , this line intersects 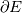 exactly twice. exactly twice. Now let's say we are solving some partial differential equation in 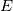 . As I understand it, for a second order problem or higher, we need to specify two (EXACTLY two) pieces of information, either both at the same point, or one at either point at which this line intersects . As I understand it, for a second order problem or higher, we need to specify two (EXACTLY two) pieces of information, either both at the same point, or one at either point at which this line intersects 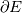 , in order to uniquely specify a solution (assuming a unique solution exists). The most common way is to use a Dirichlet condition at each point. , in order to uniquely specify a solution (assuming a unique solution exists). The most common way is to use a Dirichlet condition at each point.However, for a first order problem, (again, as I understand it) we require one, and ONLY one piece of information on this line, so the most we can do is to specify some condition at only one of these points of intersection. So, in your hexagonal domain example, boundary data on only one of the sides is enough to fully specify a solution (matching our intuition). That is essentially what I am asking about. When we specify two boundary conditions along this line for the pressure, are we just hoping that some solution exists that meets the criteria, and praying that our numerical scheme doesn't diverge? I hope this frames my question better. |
Numerical scheme diverging or not has nothing to do with the structure of the underlying continuous pde. So no need to discuss what happens numerically when you want a general answer to how many BCs you need for a given PDE.
Again you are using an example of an independent equation in E, Navier stokes is a coupled system of non-linear pde's And if this line enters and exits the same boundary.... what then? You still can have a posedness problem. Oh but you say it can't intersect itself, well a different point on the same "surface" is also not intersecting itself and can be partitioned to be a different surface via "compact surface in R3." I'm not cheating, that's what differential means. I can always carve out your surface to two smol surfaces (i.e. two points) and reduce this argument to specifying conditions at two points and not two surfaces. Furthermore, the "two" pieces of information you need to provide also aren't arbitrary for posedness. You can overconstrain a problem by specifying E everywhere depending on what the characteristics at each boundary are (the infamous static vs total properties). Consider what happens at a boundary if you have 0 velocity, + infinite velocity, and - infinite velocity. Really what matters is the Mach number, but I hope that drives the point. |
I will add that it is straightforward to prove uniqueness in a linear ODE/PDE and there you can easily show that you only need "two boundary conditions" for a 2nd-order ode/pde. But Navier-Stokes is not Laplace's equation. Furthermore, you can use a simple substitution to convert an n-order linear ode/pde into a system of n 1st order ode/pde's, i.e. starting with
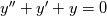 define u=y' and then you can rewrite it as define u=y' and then you can rewrite it as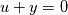 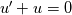 These properties make the analysis easier to generalize to higher orders for linear ODE's and PDE's because if you can show uniqueness for the 1st order case, you can then show it for the 2nd order case and so on by using this trick. But Navier-Stokes is not Laplace's equation. Let me summarize this by saying all linear 2nd order PDE's look very much alike. Coupled sets of non-linear ones don't necessarily have the same simple rules. |
Quote:
Since you are new in CFD, I suggest to stop a moment using OpenFOAM and just think about a more general statement of the problem. You have a system of equations, the divergence-free velocity constraint and the momentum equation, they should be solved as a coupled system. The hyperbolic divergence-free constraint is transformed into the elliptic Poisson equation for the "pressure" (that has nothing to do with the thermodynamic pressure) and in order for the problem to be well posed, you have to prescribe the BC along the whole frontier. The BC for the pressure is a direct derivation of the Hodge decomposition, for this reason Neumann BCs for the pressure are prescribed. However, the singularity of the matrix requires that you fulfill with your BC the compatibility condition, that is you fulfill the continuity equation. Therefore, you are wrong, the pressure equation is a governing equation substituting the continuity. |
I don't understand everything you have said, but I gather that the point you are trying to convey is "It's not so simple". I suppose all we can do is assign boundary conditions that match the physics of the problem, and hope for the best. Is that correct?
----- ADDENDUM: Why this concerns me. The momentum equation can be rewritten as 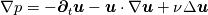 Where the right hand side side is curl-free. Let's suppose we somehow knew the solution for 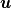 ahead of time, and all we have to do is find the pressure that fulfills our prescribed BCs. So, in general, is it possible to find ahead of time, and all we have to do is find the pressure that fulfills our prescribed BCs. So, in general, is it possible to find 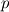 ? Essentially, we focus on the following: ? Essentially, we focus on the following:Given a connected, open, bounded subset 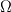 of of 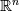 (n=2,3) and a curl-free vector field (n=2,3) and a curl-free vector field  , is it always possible to find a scalar field , is it always possible to find a scalar field  that satisfies that satisfies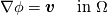  The answer is NO. For example, consider a two-dimensional case and take 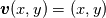 . It is easily shown that all of the . It is easily shown that all of the  that satisfy that satisfy 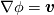 are of the form are of the form 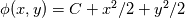 . Therefore taking for example . Therefore taking for example 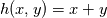 there is no solution. there is no solution. |
Interesting, and thanks for your remarks. Are you essentially saying that since the INSE are second order in u, they are basically second order in p as well by proxy? I am happy enough with this simple explanation if it is true.
|
Quote:
In some sense you are right...the formulation for the incompressible flows is somehow both not simple and not physical ... you are assuming that the pressure wave moves at infinite speed, a fact that is not physically meaningful. But it works and provides a good approximation for low Mach flows. I think you have to start from the theory of incompressible flows to understand that the "pressure" is nothing but a lagrangian multiplier. I just try to clarify the point in a different way: Assume dv/dt=a to be the eulerian acceleration and a* to be convective+diffusive terms. The system writes as Div a =0 (Continuity) a + Grad p = a* (Momentum) Now you have to consider the Helmholtz-Hodge decomposition theorem to understand that Div Grad p = Div a* is nothing but the continuity equation and the BCs are deduced by evaluating the momentum equation on the frontier dp/dn = (a*-a).n This way you have that the compatibility equation Int[V] Div Grad p dV = Int[V] Div a* dV is satisfied. That allows to have a solution apart an arbitrary function of time. In case the integral relation is not satisfied, your iterative solver will never converge. Fixing a Dirichlet condition is only a way to produce a wrong convergence, it is not necessary at all. |
about me
FYI everyone, I have a pretty extensive background in mathematics, so please feel free to communicate your ideas to me using any and all mathematical language you wish. I actually will appreciate it far better than an argument using words alone.
|
Quote:
https://www.researchgate.net/publica...ary_conditions |
I'm not sure I understand your issue but, from the original NSE one can derive a pressure equation which is a Helmholtz equation. Taking the incompressible limit, this equation collapses into a Poisson equation. I won't go into the details of which boundary conditions these equations need.
Incompressible pressure based methods do just the same, solve for a set of equations which has been artificially forced to give an elliptic nature to the pressure equation. As an additional note, we also have preconditioned density based methods, which work exactly in the opposite direction, by artificially forcing the equations to always have the compressible nature, even in the full incompressible limit, trough an artificial speed of sound. When using such methods, boundary conditions are indeed assigned following the artificially hyperbolic nature of the equations. |
Quote:
Would the compatibility equation Int[V] Div Grad p dV = Int[V] Div a* dV get satisfied if the boundary condition for p is given as dp/dn=0 and at the boundary a*.n is simply set equal to a.n? I'm assuming a*.n would need to be otherwise somehow interpolated to the boundary if cell centered FVM was used. |
Quote:
|
Very interesting! If this kind of a boundary condition is applied to the conventional
u = u*-deltaT*gradP decomposition, would this boundary condition allow to have nonzero tangential velocities prescribed at boundary aswell? Or just a nonzero normal component? |
Quote:
This is a known issue in the fractional time step method. |
Thanks for the info!
I was also wondering if this kind of a boundary condition would also work with impulsively started flows? For example if flow in a pipe was initially at rest and and then inlet velocity (say 1 m/s) was given at the the first time step, would solution of the poisson equation still enforce continuity? |
Quote:
In other words, you need to prescribe an outlet BC to ensure that the mass entering and the mass leaving are impulsively equal. In such a case the Poisson problem is well posed. |
So in theory a badly posed Poisson problem at the start would continue being badly posed through subsequent time steps and eventually even result in a solver crash?
Would a potential flow solution then be a reasonable starting point for the solver? |
The solver does not converge since from the first time step. A potential initial solution can be used.
|
| All times are GMT -4. The time now is 01:49. |