
 |
One typically writes the source term as a linearization around a 0 state (i.e., previous iteration value)
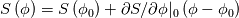 , but then the actual implementation depends from the specific method you are using (i.e., solving in delta form or not). See also https://www.cfd-online.com/Wiki/Sour..._linearization. , but then the actual implementation depends from the specific method you are using (i.e., solving in delta form or not). See also https://www.cfd-online.com/Wiki/Sour..._linearization.Hopefully, you can do 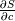 by yourself, but the possibly problematic point I see here is that the derivative is not defined at c=0 (but the source term is). Honestly, I never dealed with such problem, but a possible way out is to simply saturate the derivative at a minimum value of c (but, again, this might depend from the implemetation). by yourself, but the possibly problematic point I see here is that the derivative is not defined at c=0 (but the source term is). Honestly, I never dealed with such problem, but a possible way out is to simply saturate the derivative at a minimum value of c (but, again, this might depend from the implemetation). |
Thank you for your reply, I will read the web you mentioned.
|
| All times are GMT -4. The time now is 18:47. |