2D version of mass co-ordinate
 

It is possible to simplify the Euler equations by introducing a new set of Lagrangian co-ordinates.
, by t=t' and h is defined by:

This method has the nice property of fixing the amount of mass in an interval(this can be demonstrated by integrating the definition of h, and using the Lagrangian conservation of mass.

My question is this: Is there something similar for 2D?

http://depts.washington.edu/clawpack...system_2d.html

Recognize that x and h can be generalized to vectors and that d/dx is actually a divergence operator. In other words, it works in n-d! See Noether's second theorem.

I thought that it would be generalised from the fact that mass is conserved for the cells, the integral of the density would give the amount of mass in a particular direction.

You're literally assuming the premise when you say the question you are trying to ask is explained by itself

I think that there is an easy generalisation, you just have to use:

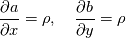Then this gives the following linear equations for the conservation of mass and momentum: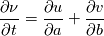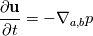


This transformation is good because it makes the convective terms disappear (like any lagrangian co-ordinate) but (hopefully) allows a fixed set of co-ordinates. like Eulerian co-ordinates.