 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Hi,
I'm trying to discretize the Navier-Stokes equation written in the spherical form for a Finite Volume formulation. I'm having problems due to the 1/r^2 terms appearing in the equation. I'm following the method of Patankar "Numerical heat transfer and fluid flow" where he integrates the equation for the control volume. It is spherically symmetric so I'm only retaining the radial terms in my equations. Does anyone know how to do this? Thanks. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
use the control volume center coordiante to compute the 1/r^2.
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
My problem is actually with integrating the equation.
I'm using Favre averaged version of the equation so I have the following convection term (1/r^2)*d/dr(r^2*rho*u*u) because u (the velocity) are functions of r I need to integrate this by parts. I tried multiplying the whole equation by r^2, but then this causes the same problem to other terms that doesn't have the (1/r^2) term. I've tried searching through the literature to find any papers that does finite volume method on spherical Navier-Stokes equation and haven't been able to find any that have done the same thing as what I'm trying to do. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
|
multiply r2 at both sides
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Thanks for the reply.
As I've already mentioned in my email, I've already tried that method. But the problem is when I multiply by r^2 on both sides I get terms like r^2*dp/dr, which again has to be integrated by parts. But since p is generally a function of r this causes problems in the integration. In addition I have more complex terms that arises due to Favre averaging such as r^2 d/dr(<rho*u''*u''>), where <> refers to Favre averages. I use the Boussinesq approximation to model this but still I get terms such as r*u, which again needs to be integrated by parts. Surely, there's another way to do this? |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
nope do not integrate by part. take r^2 is a constant
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
r^2 is not a constant, it arises by writing the Navier-Stokes equation in spherical form. r is one of the variable dimensions.
So when I'm integrating with respect to r, r^2 can't remain a constant. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Jul 2009
Posts: 353
Rep Power: 18  |
I'm not sure I'm following what you are actually trying to do at this point. It sounds as if you are trying to integrate the full Navier-Stokes equations analytically. If you want to do a finite volume discretization, then the 1/r**2 term will be a part of what you discretize - in that case you will use the value at the cell center, as ztdep has suggested. Treat it just like any other term in the discretized equation.
|
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Sorry I should've explained it a bit more clearly
So I have the following 1-D Navier-Stokes equation written in spherical coordinates 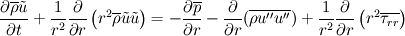 where 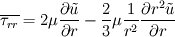 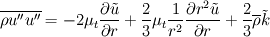 Now what I want to do is integrate this momentum equation over the control volume and over time. Since it's 1-D I only consider a control volume around a single grid point P, the grid point East of point P is referred to as E and to the West is referred to as W. Let's say I want to integrate the term 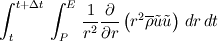 If the 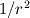 term wasn't there this would have been straightforward, which is the case in the Cartesian coordinates. term wasn't there this would have been straightforward, which is the case in the Cartesian coordinates. So one thing I tried to do was to multiply the whole equation by 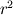 . But then I get terms like . But then I get terms like 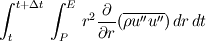 which again gives me the same problem. This may be different to what's normally done in Control Volume analysis. I'm trying to use the method of Patankar "Numerical Heat Transfer and Fluid Flow", 1980. Thanks. Last edited by lost.identity; April 16, 2010 at 11:19. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
|
r^2 tem represent the element volume in the sperical coordinate system Dv. as in cartesian coordinate, it is 1 dx dy dz.
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Thanks, I think I sort of know what you're saying.
Are you saying that when I multiply by 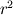 , and integrate then terms such as , and integrate then terms such as![\int_P^E\,r^2\frac{\partial}{\partial{r}}(\overline{\rho{u''}{u''}}) \,dr= \Delta{V}\left [ (\overline{\rho{u''}{u''}})_E-(\overline{\rho{u''}{u''}})_P \right ] \int_P^E\,r^2\frac{\partial}{\partial{r}}(\overline{\rho{u''}{u''}}) \,dr= \Delta{V}\left [ (\overline{\rho{u''}{u''}})_E-(\overline{\rho{u''}{u''}})_P \right ]](/Forums/vbLatex/img/e5cd45581cc9c33784336f4e3808bb69-1.gif) is this true for 1-D case such as mine? and would 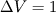 ? ?or is 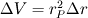 where 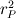 is the radial value at the mid-point of the control volume? is the radial value at the mid-point of the control volume?
Last edited by lost.identity; April 16, 2010 at 15:42. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
|
yes, that is what i mean/
by the way , how do you input the formular? |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
||
|
|

|
|
|
|
|
#14 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
||
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Filtered navier stokes equation..LES:: | Palani Velladurai | Main CFD Forum | 7 | September 6, 2013 02:51 |
| Navier Stokes, Pressure BC, Discretization | Sree | Main CFD Forum | 0 | August 1, 2007 04:55 |
| Navier stokes compresible viscid flow fea, somebody can help? | Jose Choy | Main CFD Forum | 3 | October 24, 2003 02:28 |
| Newbie:Viscoelasticity and Navier stokes equation | Rajil Saraswat | Main CFD Forum | 2 | June 9, 2003 07:21 |
| help: I am trying to solve Navier Stokes compressible and viscid flow | Jose Choy | Main CFD Forum | 2 | May 18, 2000 05:45 |