
 |
Check out: http://www.cfd-online.com/Wiki/Einst...ion_convention
The LHS you have written is also a scalar and uses the Einstein summation convention |
Quote:
The difficulty is that the index does not repeat in any individual term, we don't have any summation. http://topex.ucsd.edu/geodynamics/shearer.pdf this is about solid mechanics, but those concepts such as strain tensor and rotation tensor also apply to fluid mechanics. |
Actually, (dui/dxj + duj/dxi)*dui/dxj = (dui/dxj)² + duj/dxi*dui/dxj
Now, you have two terms in which the indexes repeat themselves. Therefore, there is a summation on both i and j for each terms After a few step, you will get the RHS from the LHS in your first post |
|
I think you're right in the way you wrote the expressions of
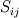 and and 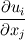 However, you're mistaken in the fact that 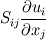 is not only a product of matrices when using Einstein's convention: you have to sum over i and j, which corresponds to computing the trace of the matrix. is not only a product of matrices when using Einstein's convention: you have to sum over i and j, which corresponds to computing the trace of the matrix.Let me show you. I won't develop the Stress tensor, and I will call each of its components S11, S12.... Let's start with the Einstein's summation convention 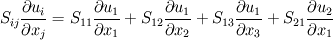 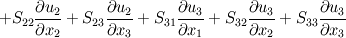 That will eventually lead to the RHS term you wrote in your first message Without the convention, it would be a classical matrix product between two 3x3 matrices, yielding a 3x3 matrix as well. If we call it M, we have 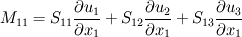 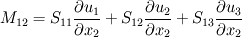 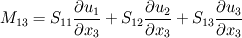 and so on for the next lines. We can notice that the RHS term only contains the sum of the diagonal terms of M. Therefore, if you prefer to use the matrix product rather than the Einstein convention to compute and develop your term, you just have to remember that this convention is equivalent to the computation of the trace of the resultant matrix Here we are. I hope it will help a little Cheers Guillaume |
Thank you for your explanation. This is very helpful discussion.
Quote:
|
| All times are GMT -4. The time now is 10:22. |