CFD Online Discussion Forums - 1-D spherical finite volume discretisation

I'm trying to discretise the conservative equations using FVM for a 1-D spherical geometry (i.e. spherical symmetry).

After applying the Gaus's theorem I get the following for spatial discretisation of the diffusive terms

$\boldsymbol{\Gamma_f}\cdot\boldsymbol{A}_f$

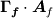
I know that for 1-D Cartesian the face area vector is simply 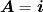$\boldsymbol{A}=\boldsymbol{i}$ where i is the unit vector in the x-direction.

However, what will be the face area vector for a spherical geometry? Surely it can't just be the unit vector.

I know that the area element in spherical coordinates is given by

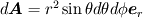$d\boldsymbol{A} = r^2\sin\theta{d}\theta{d}\phi\boldsymbol{e}_r$ symbol. So in 1-D can I assume it to be just r^2?

Thanks.