CFD Online Discussion Forums - Velocity correction and under-relaxation in the SIMPLE algorithm

CFD Online Discussion Forums (https://www.cfd-online.com/Forums/)

- Main CFD Forum (https://www.cfd-online.com/Forums/main/)

- - Velocity correction and under-relaxation in the SIMPLE algorithm (https://www.cfd-online.com/Forums/main/81088-velocity-correction-under-relaxation-simple-algorithm.html)

Velocity correction and under-relaxation in the SIMPLE algorithm

Dear all.
Please bear with me as I am a beginner to the field of CFD.

My question concerns the update of velocities in the SIMPLE algorithm. Specifically, I am wondering how the update is done when under-relaxation of both momentum and pressure is implemented. In the SIMPLE algorithm the velocity correction comes up by substracting the guessed velocity field with the "correct" velocity field (that satisfies the momentum equation). For the u-velocity in a cubic control volume:

$\frac{a_P}{\alpha_m} u^{*}_{P} = \sum a_{nb}u^{*}_{nb}-(p^{*}_{e}-p^{*}_{w})A+(1-\alpha_m)\frac{a_P}{\alpha_m}u^{*,0}_{P}$

substracted from:

$\frac{a_P}{\alpha_m} u_{P} = \sum a_{nb}u_{nb}-(p_{e}-p_{w})A+(1-\alpha_m)\frac{a_P}{\alpha_m}u^{0}_{P}$

results in:

$\frac{a_P}{\alpha_m} (u_{P}-u^{*}_{P}) = \sum a_{nb}(u_{nb}-u^{*}_{nb})+\left[(p_{w}-p^{*}_{w})-(p_{e}-p^{*}_{e})\right]A+(1-\alpha_m)\frac{a_P}{\alpha_m}(u^{0}_{P}-u^{*,0}_{P})$

The correction is then

$u^{'}=u-u^{*}$ for the velocity and
$p^{'}=p-p^{*}$ for the pressure.

Now as far as I understand it, you discard the sum terms (neighbors). However, after reading Versteegs book, I still do not understand what happens to the under-relaxation term. In Peric, Kessler and Scheurer (1988), Computers & Fluids, 16,4, p. 384-403, it seems that the term $u^{0}-u^{*,0}$ does not even appear and we're left with:

$u^{'}=\frac{p^{'}_{w}-p^{'}_{e}}{\frac{a_P}{\alpha_m}} A$

Is this true?

Furthermore, what happens to the pressure under-relaxation factor $\alpha_p$ ? Should it be included before the velocity correction equation above?

I would be grateful for a clarification

Regards
Johnhelt

correction is just a rough approximation to conservation equations.
when you apply the SIMPLE algorithm to solve a problem, under relaxation factor will be used to calculate the velocity and it does not make a sence to be applied again in velocity correction step.
for example, consider that you have a very complex geometry and you are obliged to use a very small under relaxation factor, say 0.1,.
if you apply this factor to momentum equation it will reduce convergence rate considerably but it has no influence on the converged velocity field. but now imagine that you apply 0.1 in the correction step. what will happen? u' or P' will recieve a huge unrealistic change and it may leads in divergence.

Thank you for the reply, I'm not sure, however, I understand 100%...

You say that introducing under-relaxation may lead to too high velocity change/correction. As I see it, if I have velocity under-relaxation then 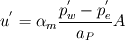$u^{'} = \alpha_m\frac{p^{'}_{w}-p^{'}_{e}}{a_P}A$ should decrease with increasing under-relaxation...

And, if I then apply the pressure under relaxation factor I get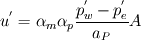
$u^{'} = \alpha_m\alpha_p \frac{p^{'}_{w}-p^{'}_{e}}{a_P}A$ , which then decreases the velocity correction even further.

In the end, of course, it should not matter for a converged solution. However, to get there is the key issue :-)

Regards