
 |
Viscous term in Navier Stokes Equations
|
Hi
The first one corresponds to non-dimensonalized equations, and the second one in dimensional form |
I have also come across a third form of the viscous term
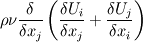 ("Benchmark Computations of Laminar Flow around a Cylindr", Schafer and Turek; 1996, Notes on numerical dluid mechanics; 52, 547-566) ("Incompressibel Fluid Dynamics", Hunt; 1964) this seems to relate directly to the visous fluid stress tensor, 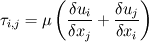 ("Introduction to computational fluid dynamics", Date; 2005) as far as I can tell this adds another three elements to the viscous term, so for a three dimensional flow the term would be, 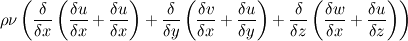 the connection to the stress tensor seems logical, however I cand seem to find a direct derivation. Inconsistancy between available literature sources seems to be sending me in circles, Can anyone help me figure out which formulation I need? Dan |
The same equation can be written in many ways. CFD Wiki provides a more general dimensional form, which is valid for compressible flows (some of your examples assume incompressible flow):
http://www.cfd-online.com/Wiki/Navier-Stokes_equations |
Hi Pete,
I'm still strugelling to see the equivelence the link you posted gave the viscos term for the ith dimension as, 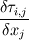 which agrees with the formulation in my last post, yet how can this be equivelent to the formulations in my original post, if the entire rest of the equation of momentum matches up, except for the three added terms, 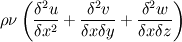 Unless these terms all cancel out to zero..or I'm simpy interpreting the notation incorrectly. |
Hi
your \tau_{ij} term has a missing term. According to stokes hypothesis for a Newtonian fluid \tau_{ij} = \left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i} - \frac{2}{3}\frac{\partial u_i}{\partial x_j}\delta_{ij} and apply divergence to this quantity |
|
Quote:
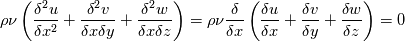 |
| All times are GMT -4. The time now is 00:21. |