
 |
Volume averaging in cell
Dear OpenFOAM users,
I solved a flow problem over and array of cylinders: https://www.dropbox.com/s/v5nz4mvx6user06/6-4_cell.png I would like to get the volume average of the velocity and pressure fields over a limited, moving volume (typically the size of a single cell, see the mask on the screenshot). The resulting field would be continuously defined over the entire domain, including in the cylinders. This is field volume averaging / spatial frequency filtering, in the sense of Whitaker (1999) and is somehow like the spatial averaging operation used for LES theory. Do you think it is possible to do this while solving the problem or as a post-processing operation? I didn't find a way to apply such a moving filter in Paraview or in the sample utility, and I don't know how to program this in a solver. |
Update
Additional (maybe simpler) question: How to export the fields to that kind format:
x y z Ux Uy Uz p with (x,y,z) coordinates on a cartesian grid. Just doing that would be sufficient, the computation of the average being possible as a post-processing operation. |
Solution (non optimal)
1 Attachment(s)
After a week of hacking (or so), I put together a solution. I forked simpleFoam and added this piece of code in it:
Code:
{Handling multiprocessor cases is critical, and I found the solution there: http://www.cfd-online.com/Forums/ope...ral-mag-u.html I believe there's a bottleneck at the filter setting operation, which is not parallelized. |
Use of LES filters?
Dear foamers,
Does anyone know if an LES filter wouldn't be suitable to do this? I can't exactly understand what the simpleFilter, laplaceFilter, and such, do. |
OK. I see this thread is rather old but still...
I implemented some explicit filtering/moving average, too. It works in parallel but takes ages. And edge effects are also an issue with this filtering stuff. So here's what I'm doing now: In k-space (wave number), the frequency response of a moving average filter (rectangular impulse response) is a sinc function: <phi> = sin(L/2*k)/(L/2*k) phi for a generic variable phi, filter length L and brackets <> denoting filtering. you can express this as an infinite series: sinc(L/2*k) = sum_n [L/2*(i*k)]^(2*n) /[(2*n+1)!] for n from zero to infinity. Note that (i*k)^2 is essentially the Laplacian. Now let's write this in a recursive manner: At iteration m <phi>_m = <phi>_(m-1) + (L/2)^2/[2*m*(2*m+1)] Laplacian[<phi>_(m-1)] This is basically the heat equation with a time-dependent diffusivity (tau is the numerical time step) d<phi>/dt = (L/2)^2/tau /[2t/tau*(2t/tau+1)] Laplacian[<phi>] Actually, from the series expansion we get Explicit Euler time integration which is numerically unstable unless Diffusion number is very small. Although it's mathematically not that sound, I just use implicit time integration here. Remember this is "pseudo time". You have to run this until some steady state at every real time step. But Laplace Equation is easy to solve and as the diffusivity decreases with time it should converge rather quickly. Edit: This derivation is for 1D. Physically it makes sense, I think. But I'd be glad if someone could comment on the multidimensional problem... |
Hi Sebastian,
This way of doing things seems quite elegant to me. However, there are a few things that remain unclear to me. I'm going to do a more detailed development of the calculus, using proper math notations for more clarity. That will help me explain where the things I don't understand are. We start with a given field 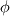 we want to get the average of using what I'll call the we want to get the average of using what I'll call the 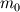 top-hat filter of width top-hat filter of width 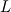 : :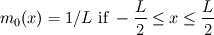 and 0 otherwise. Note that this filter is the first of a family of recursively defined filters that have interesting properties regarding control of the regularity of the resulting averaged field (see Angeli et al., 2013). We get the average field 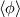 by applying the by applying the 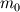 filter using a convolution operator. filter using a convolution operator. 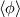 's expression in 's expression in  is: is: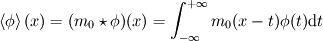 Now, we go to the phase space by applying the Fourier transform operator 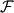 : : = \mathcal{F}[m_0](k) \ \mathcal{F}[\phi](k) \mathcal{F}[\left< \phi \right>](k) = \mathcal{F}[m_0](k) \ \mathcal{F}[\phi](k)](/Forums/vbLatex/img/90510811de2ae93eb8c8631fef9af76f-1.gif) where 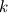 is the wave vector. is the wave vector.The only problem-independant thing we have here is the Fourier transform of the filter. As you mentioned, the Fourier transform of 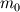 is a sinc: is a sinc: = \mathrm{sinc}\left(\frac{kL}{2}\right) \mathcal{F}[m_0](k) = \mathrm{sinc}\left(\frac{kL}{2}\right)](/Forums/vbLatex/img/1b1b2c3ae04863001bc60663ff9072b8-1.gif) and its Taylor series expansion is 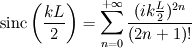 This gives us the following expression for ![\mathcal{F}[\left< \phi \right>] \mathcal{F}[\left< \phi \right>]](/Forums/vbLatex/img/96bd1328f59ce6d9c8304797308afab6-1.gif) : : = \sum_{n = 0}^{+\infty} \left( \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k) \right) = \lim_{n \rightarrow +\infty} S_n \mathcal{F}[\left< \phi \right>](k) = \sum_{n = 0}^{+\infty} \left( \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k) \right) = \lim_{n \rightarrow +\infty} S_n](/Forums/vbLatex/img/eb32f871e69d99d337a93bd658595e11-1.gif) where  S_n = \sum_{m=0}^n \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k)](/Forums/vbLatex/img/f8c88e3a9a6d4263d39fd51dc9fd0cc4-1.gif) For there, we can move to a recursive definition of the 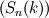 sequence: sequence: S_n(k) = S_{n-1}(k) + \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k)](/Forums/vbLatex/img/fe83a854c629594a7fdd23c1e2364d80-1.gif) with the initial condition  S_0(k) = \mathcal{F}[\phi](k)](/Forums/vbLatex/img/3d415d2fc983d07ba15b76f3e262b008-1.gif) Finding the limit of the 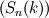 sequence would clearly give us sequence would clearly give us ![\mathcal{F}[\left< \phi \right>] \mathcal{F}[\left< \phi \right>]](/Forums/vbLatex/img/96bd1328f59ce6d9c8304797308afab6-1.gif) , indeed. What I don't understand at this point is how you proceed to the laplacian-based formulation you provide: the , indeed. What I don't understand at this point is how you proceed to the laplacian-based formulation you provide: the 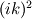 product meaning "apply laplacian" only works if you go back to the real space, in which the recursive definition doesn't work. Plus, we don't have product meaning "apply laplacian" only works if you go back to the real space, in which the recursive definition doesn't work. Plus, we don't have 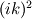 in the recursive definition; only in the recursive definition; only 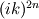 , a lot less convenient. Did I miss something? , a lot less convenient. Did I miss something?I've also been trying to write this for a 2D problem, but I couldn't figure out how to get to a recursive expression for the Taylor series terms, mostly because the Fourier transform of the 2D  filter is a product of two Taylor series (I'm not a good mathematician). filter is a product of two Taylor series (I'm not a good mathematician). |
| All times are GMT -4. The time now is 19:33. |