
 |
laplacianFoam: problem with fvc::laplacian
2 Attachment(s)
Dear OpenFOAM users,
I am developing a solver for a 1D application. I started with laplacianFoam as a base, and at some point, I had to introduce a source term which is a combination of laplacian(DT, T) in some cells and and some other computations in the others (impossible to use partitioning into regions because the cells concerned by the special computations change dynamically). Since I could not mix implicit and explicit terms, I decided to go fully explicit and used fvc::laplacian(DT, T). This resulted in a crash of the solver. On the forum, I saw that people having that problem usually have it solved by simply changing the numerical scheme; however, in the case of that 1D example, it does not seem to make a difference. I investigated using a minimal working example attached to this post. It is made of:
Question: Does someone have an idea of what is happening? PS: In case that would be of any help, I should also mention that in the practical example I am dealing with (not the MWE), the source term wiggles very oddly and explodes when going in the direction of the "hot" wall. I attached a screenshot of postprocessed data: in blue is the initial source term (non-zero, but small intensity compared to the green curve) and in green is the source term after the first time step. |
Hi Tobias,
Thank you very much for this thorough answer. Sometimes, I get lost in the complicated stuff and even forget about the most elementary things. Coming back to my original problem: my conservation equation is 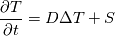 where 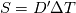 in some regions and is gotten from another solver elsewhere. How come the laplacian part of in some regions and is gotten from another solver elsewhere. How come the laplacian part of 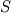 affects the stability of the problem? Does this mean that not satisfying the stability criterion results in practice in (very) wrong values of the explicitly evaluated laplacian operator? affects the stability of the problem? Does this mean that not satisfying the stability criterion results in practice in (very) wrong values of the explicitly evaluated laplacian operator? |
| All times are GMT -4. The time now is 21:37. |