
 |
discrepancy in fvc::grad(U)
HI all,
Recently I noticed that in openfoam, gradient of a vector is computed as the outer product of the gradient operator and the vector. Page 25 (bottom) of the programmer's guide defines the gradient of velocity field as: which is transpose of what we exactly mean by grad(U) as: I checked the computed values of gradient of velocity field near the wall (where wall normal component is expected to be dominant) and I can confirm that it outputs the transpose of what we actually want. To my surprise, I have seen people use the grad(U) without taking its transpose in openfoam that would actually give the correct tensor. Has anybody encountered this issue before? OpenFOAM Version: 2.4.0 |
Hello,
The result is correct however the notation of the manual is confusing (wrong). The problem is due to the nabla operator (  ). ).because by convention [Ref. 1] (look carefuly to the position of the indices): 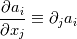 Why? because in this context, 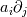 will not make sense (remember that the operator nabla must act on the vector will not make sense (remember that the operator nabla must act on the vector 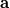 so it must be at the left). so it must be at the left).Conclusion: The gradient is calculated correctly (matrix form), but the notation ( 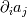 ) given in the manual for the gradient is wrong (it is for the transpose of the gradient). ) given in the manual for the gradient is wrong (it is for the transpose of the gradient).[Ref. 1]: See page 7 of this document: http://web.iitd.ac.in/~pmvs/courses/mcl702/notation.pdf |
|
Quote:
This is what we actually need (the common agreed upon definition of velocity gradient in all textbooks on fluid mechanics): Code:
U1,1 U1,2 U1,3Code:
U1,1 U2,1 U3,1 |
This is a matter of layout convention. You can take a look to this detailed section on wikipedia.
Your notation: Quote:
|
Quote:
The issue was just to make it very known that with using fvc::grad(U) in foam, as I said, we are not computing the gradient as the textbook definition used for gradient of velocity is written. I have seen people use it right away in calculations when they actually were meant to use its transpose. So care must be taken! Thanks for your time!! I am pretty sure that this discussion will help a lot of people! |
|
No it is not wrong. It expands to a tensor that you mentioned in your second comment to this thread which is the correct form of gradient.
|
Hello,
I also encountered this issue. In my opinion, fvc::grad computes the transpose of the gradient... It is well documented in the programmers' guide - p25 eq2.3. |
No, I think that the OpenFOAM notation does hold up, and makes more sense to me.
For example, the outer product of two vectors, 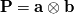 , can be written in terms of matrix multiplication as , can be written in terms of matrix multiplication as 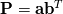 . .Now apply that to the grad operation, which is the outer product of nabla and the vector: 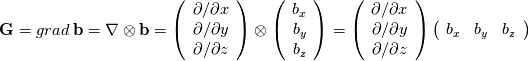 which on multiplying out gives: 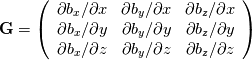 and hey presto you get the convention that OpenFOAM uses. Just as a reminder, the middle term on the top row is component 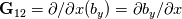 . You just need to remember that the nabla operator comes before the thing it operates on, and so its index comes first. . You just need to remember that the nabla operator comes before the thing it operates on, and so its index comes first. |
Also, we are not much bothered about the convention. We are more concerned about the correct implementation of the terms that arise in FD equations. I think the best practice to address this is to be careful what the term that you are trying to implement involves -- whether you want [U1,1 U1,2 U1,3; U2,1 U2,2 U2,3; U3,1 U3,2 U3,3 ] to be implemented or its transpose. The implementation of gradient in FOAM is technically its transpose but in most of the fluid dynamic equations the tensor I just wrote above is more common representation of (del/del_xj U_i).
|
|
1 Attachment(s)
Quote:
As for your Reynolds stress production terms, see the attached image for the OpenFOAM notation way of writing this (I ran out of patience with trying to do the notation in this editor!). Hope that helps ... Note: some of the terms in the last matrix are wrong - see the corrected version below |
Quote:
Correct, that is how I would implement the first term. Would the second term implementation be any different? I would write the second term as: (with the velcoity gradient getting pre-multiplied) 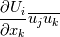 with the stress tensor and your velocity gradient tensor transposed as: 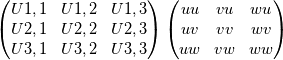 Do you agree? |
1 Attachment(s)
|
According to my own test. I confirm that OpenFoam uses the transpose of the jacobian matrix for the gradient of a vector.
I think that it should be written somewhere because when you derive your own equation using the classical jacobian matrix it can be a source of error very hard to catch if you code it without knowing it. |
The treatment on the grad is confusing in my opinion.
Just imagine you compute "skew(gradU)" by assuming the traditional notation. |
| All times are GMT -4. The time now is 20:30. |