
 |
Error in magneticFoam ??
Dear Foamers,
After going through the code for magneticFoam, and several other threads in the forum I manage to understand a bit of its working (I might be completely wrong as well:D). As per the source code, the magneticFoam solves the Gauss's law for magnetism ( 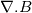 ) to produce a divergence free field. To obtain this, it uses a scalar potential ( ) to produce a divergence free field. To obtain this, it uses a scalar potential (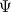 ) formulation and gradient of this volScalarField (which will be volVector) is then defined as strength of magnetic field ( ) formulation and gradient of this volScalarField (which will be volVector) is then defined as strength of magnetic field (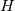 ) )The solution of 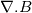 where where 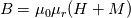 is written in source code as is written in source code as Code:
solve(fvm::laplacian(murf, psi) + fvc::div(murf*Mrf))After solving the above equation,  is then used to construct the H field ( is then used to construct the H field (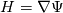 ) as ) as Code:
fvc::reconstruct(fvc::snGrad(psi)*mesh.magSf())Further B is also constructed in the similar fashion using 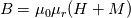 Code:
constant::electromagnetic::mu0*fvc::reconstruct(murf*fvc::snGrad(psi)*mesh.magSf() + murf*Mrf)Now, the reason to go for the scalar potential formulation rather than vector one might be because scalar potential formulation automatically satisfies the Ampere's law ( 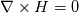 ) for electrically insulating media, as the curl of gradient of scalar is always zero ( ) for electrically insulating media, as the curl of gradient of scalar is always zero (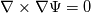 ). ).Now, here comes the interesting part, the geometry of magnets is defined using faceSet in toposet and then all the faces are assigned the same values of relative permeability (murf) and remanance (Mrf). This is achieved with the following line in createFields.H Code:
forAll(faces, i)Code:
Sf[facei]This means the magnitude of surface area of every cell face is multiplied with Mr to define the Mrf , which is then further used to calculate 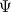 and reconstruct and reconstruct 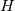 . So, as the grid becomes finer the corresponding value of surface vector reduces and so does the Mrf. This makes the magnetic field distribution grid dependent :confused: . So, as the grid becomes finer the corresponding value of surface vector reduces and so does the Mrf. This makes the magnetic field distribution grid dependent :confused:This strange behaviour can be easily observed by just increasing the mesh from 100*100*100 to 200*200*200 in the magnetic_rectangular case of https://www.cfd-online.com/Forums/op...tml#post773442 It'll be really helpful if someone can confirm/contradict this and make the source code more clear for all of us. |
Very interesting. Thanks for detailed inspection.
I am no expert on magnetism. But, if your observations are correct, what could be the fix? Is there any minimal reproducible verification/validation test scenario in the literature, with which we can do tests? |
1 Attachment(s)
Quote:
Regarding the verification/validation test scenario in the literature. So far I just came across following analytical expression for on-axis magnetic field distributions https://www.supermagnete.nl/eng/faq/...t-flux-density Much more detailed 3D distributions (but only for rectangular magnets) can be obtained from the equations 12 - 14 of the following paper https://link.springer.com/content/pd...BF02437333.pdf Now to get first hand idea, if we use the analytical formula to calculate the field distribution for 20mm long (L), 20mm wide (W), 40mm tall (D) having Br = 860KA/m & unit relative permeability (this specific configuration as it was readily available test case from https://www.cfd-online.com/Forums/op...tml#post773442). The distribution shows highest magnitude of around 4.5e5 A/m as shown in attached figure... However, if we run the same configuration in FOAM (using the default source code) we get LOWEST value of B is of order e8...which is definitely not correct... Coming to the The "fix"..... I tried to normalise the Mrf with its face area magnitude using Code:
Mrf[facei] = (Mri*(orientationi & Sf[facei]))/(mag(Sf[facei]));Some things to be aware of: 1) As already put out on the forum, the dimension of magnet is set by topoSetDict whereas the bounding box is defined using blockMeshDict. 2) The constant/transportProperties can only be used to define the orientation of the magnet, the Mrf & Mur has to be changed from createFields.H. This should be followed by wclean+wmake... P.S. Unfortunately, at this moment I'm unable to attach any zip files bcz of a error "submission could not be processed because a security token was missing." |
| All times are GMT -4. The time now is 15:27. |