 |
|
|
[Sponsors] | |||||
nonlinear equation with non-constant (nonlinear) and direction dependent diffusion |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Mieszko Młody
Join Date: Mar 2009
Location: POLAND, USA
Posts: 145
Rep Power: 17  |
Dear Foamers,
I am trying to solve/implement nonlinear equation with non-constant (nonlinear) and direction dependent diffusion. It looks like that: Equation is solved for 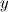 in rectangular in rectangular 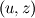 domain: domain:![\frac{\partial y}{\partial t} + \frac{\partial \psi}{\partial z} = \frac{\partial^2 y}{\partial z^2} + \left[ \frac{1+(\frac{\partial y}{\partial z})^2}{(\frac{\partial y}{\partial u})^2}\right] \frac{\partial^2 y}{\partial u^2}
- 2 \left[ \frac{\frac{\partial y}{\partial z}}{\frac{\partial y}{\partial u}}\right] \frac{\partial^2 y}{\partial z \partial u} \frac{\partial y}{\partial t} + \frac{\partial \psi}{\partial z} = \frac{\partial^2 y}{\partial z^2} + \left[ \frac{1+(\frac{\partial y}{\partial z})^2}{(\frac{\partial y}{\partial u})^2}\right] \frac{\partial^2 y}{\partial u^2}
- 2 \left[ \frac{\frac{\partial y}{\partial z}}{\frac{\partial y}{\partial u}}\right] \frac{\partial^2 y}{\partial z \partial u}](/Forums/vbLatex/img/8df7c1f42819ed9f2bde234f12e8379d-1.gif) I decided to solve it as follows: fvScalarMatrix yEqn ( fvm::ddt(y) - U.component(1) - fvm::laplacian(nu + (A/C)*nu2, y) + D/C ); where: nu and nu2 are defined to act in z and u directions respectively nu = (1 0 0 0 0 0 0 0 0) and nu2 = (0 0 0 0 1 0 0 0 0 0), and 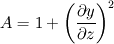 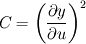 and ![D = 2 \left[ \frac{\partial y}{\partial z}\frac{\partial y}{\partial u}\right] \frac{\partial^2 y}{\partial z \partial u} D = 2 \left[ \frac{\partial y}{\partial z}\frac{\partial y}{\partial u}\right] \frac{\partial^2 y}{\partial z \partial u}](/Forums/vbLatex/img/2158a05ad616ad2b084c417d13395d60-1.gif) and 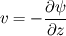 , (vertical velocity) , (vertical velocity)where A, C and D are solved explicitly. But solver had a problem with it, because C were getting too large. So I decided to multiply above equation by C and get: fvScalarMatrix yEqn ( C*fvm::ddt(y) - C*U.component(1) - fvm::laplacian(C*nu + A*nu2, y) + D ); Here I got solution, somehow similar to the one it should converge, but not exactly. Problem seems to be in "C*fvm::ddt(y)" term, because it gives me the same answer if I have just "fvm::ddt(y)" ... Any idea, what can be here wrong, or how to make it better ? Thanks ZMM |
|
|
|

|
|
 |
| Tags |
| direction dependent diff, non-constant diffusion, nonlinear diffusion, nonlinear equation |
|
|