[aylalisa]

Dear All,

I'd like to simulate the following case:

A duct with a relatively big aspect ratio W/H (big width, small height).
Water flows through the duct, forced by a given pressure difference.
Thermal energy is led to the fluid via the bottom area of the duct.

Which solver from the category 'Heat transfer and buoyancy-driven flows' do you suggest and why?

Thanks to everybody!

Aylalisa

[RMF]

It depends on the exact parameters of your simulation. If buoyant effects are significant in your case you need to use one of the buoyant solvers. If the change in the density due to the temperature differences is small you can use one of the buoyantBoussinesq solvers. To get an estimation of the influence of the buoyancy you can use the ratio of Grashof to Reynolds^2.

If the temperature difference is large and you can neglect buoyant effects, you can use the rho* solver (e.g. rhoSimpleFoam).

Hope it helps
RMF

[aylalisa]

Originally Posted by RMF

It depends on the exact parameters of your simulation. If buoyant effects are significant in your case you need to use one of the buoyant solvers. If the change in the density due to the temperature differences is small you can use one of the buoyantBoussinesq solvers. To get an estimation of the influence of the buoyancy you can use the ratio of Grashof to Reynolds^2.

If the temperature difference is large and you can neglect buoyant effects, you can use the rho* solver (e.g. rhoSimpleFoam).

Hope it helps
RMF

Hi RMF,

thank you very much for your reply!

Concerning my case I have to account for...
- buoyant effects due to the thermal energy applied through the bottom plate (I think?)
- laminar flow, transition to turbulent flow because of applied thermal energy (I think?)

Therefore I guess I can exclude "buoyantSimpleRadiationFoam" solver and
"chtMultiRegionFoam" solver.

The remaining solver denotations confuse me:

buoyantBoussinesqPimpleFoam:
Transient solver for buoyant, turbulent flow of incompressible fluids
buoyantBoussinesqSimpleFoam:
Steady-state solver for buoyant, turbulent flow of incompressible fluids

My understanding so far:
Boussinesq-Approximation means a change in density due to temperature changes, not because of pressure changes.
The density changes are considered in the buoyancy term. I have temperature differences, hence buoyant effects.

The solver description says: "....buoyant, .....flow of incompressible fluids"
I was of the mind that "incompressible" means no change in density. But "buoyant effect" means temperature differences cause density changes. How can I have buoyant effects in an incompressible fluid?

You say that buoyancy can be neglected if temperature differences are large. I thought that big temperature differences cause high density changes and therefore a a large buoyant effect???

boyantBaffleSimpleFoam:
steady-state solver for buoyant, turbulent flow of compressible fluids using thermal baffles

What occasions demand thermal baffles?

buoyantPimpleFoam
Transient solver for buoyant, turbulent flow of compressible fluids for ventilation and heat-transfer

Does "ventilation and heat transfer" bear on gaseous fluids and forced convection, for example with a fan ?
For that case I could exclude the "buoyantPimpleFoam" solver as well.

buoyantSimpleFoam
Steady-state solver for buoyant, turbulent flow of compressible fluids

Because of my mentioned objections I would go for the "buoyantSimpleFoam" solver for my case at the moment.


Could you try to answer my questions for the sake of my better physical understanding???



Aylalisa

[RMF]

Hi Aylalisa,

now your problems are getting clearer for me and I know what to explain.

Boussinesq-Approximation means a change in density due to temperature changes, not because of pressure changes.

The Boussinesq-Approximation means that the changes in density (due to temperature change) are very small. So the change of density is only taken into account in the term of the buoyant force. The change is neglected in every other term of the Navier-Stokes-Equation (e.g. convection term etc.). This approximation is only valid for small density changes (Wikipedia says it becomes innaccurate when DeltaRho/rho is of order unity).

I was of the mind that "incompressible" means no change in density. But "buoyant effect" means temperature differences cause density changes. How can I have buoyant effects in an incompressible fluid?

Incompressible in this case means (and I think in general) that the density is not influenced by pressure. That does not exclude that the density changes because of a temperature change.

The buoyantBoussinesq solver use an expansion coefficient to describe the density change caused by temperature. Therefore they do not take the pressure effects into account.

You say that buoyancy can be neglected if temperature differences are large.

Sorry, that's actually not what I wanted to say. These two things were both conditions: if your temperature difference is large + if you can neglect buoyant effect, then you can use the rho* solvers. I hope this makes it clear. But I got from your reply, that you want to analyse buoyant effects, so you can't use the rho* solvers anyway.

I didn't even know that there is a buoyantBaffleSimpleFoam...so I can't help you with that.

buoyantSimpleFoam and buoyantPimpleFoam are the same class of solvers (concerning the physics of the flow). The Pimple version is for unsteady problems whereas the Simple version is for steady state problems. These two are the general solvers for heat transfer problems (natural and forced convection), if you can't use the Boussinesq-Approximation. They can be used in cases of large density variation and the can take the compressibility into account.

I would take a look at the maximum expected relative density change in your case. If it is small I would use the boussinesq Solvers -> buoyantBoussinesqSimpleFoam (believing you have an steady state case)

If the Boussinesq-Approximation is not valid in your case, you will have to use buoyantSimpleFoam.

Bye RMF

[aylalisa]

Hi RMF,

please forgive me my unnerving inquiry .
Your answers have boosted my idea up to a big extent!!!

There is one remaining point I am still not clear about.

Originally Posted by RMF

Hi Aylalisa,

now your problems are getting clearer for me and I know what to explain.



The Boussinesq-Approximation means that the changes in density (due to temperature change) are very small. So the change of density is only taken into account in the term of the buoyant force. The change is neglected in every other term of the Navier-Stokes-Equation (e.g. convection term etc.). This approximation is only valid for small density changes (Wikipedia says it becomes innaccurate when DeltaRho/rho is of order unity).


Incompressible in this case means (and I think in general) that the density is not influenced by pressure. That does not exclude that the density changes because of a temperature change.

The buoyantBoussinesq solver use an expansion coefficient to describe the density change caused by temperature. Therefore they do not take the pressure effects into account.



Sorry, that's actually not what I wanted to say. These two things were both conditions: if your temperature difference is large + if you can neglect buoyant effect, then you can use the rho* solvers. I hope this makes it clear. But I got from your reply, that you want to analyse buoyant effects, so you can't use the rho* solvers anyway.

Here is my problem:
I understood that both statements are conditions. And that is the point I don't get.
If the temperature difference is large, then, I've assumed so far, that the changes in density must be large and the effect on the buoyancy term must be large, too. How can I, under these circumstances, neglect the buoyant effect?
Does a rho*solver buoyant effects not take into regard in the equations?

Originally Posted by RMF

I didn't even know that there is a buoyantBaffleSimpleFoam...so I can't help you with that.

buoyantSimpleFoam and buoyantPimpleFoam are the same class of solvers (concerning the physics of the flow). The Pimple version is for unsteady problems whereas the Simple version is for steady state problems. These two are the general solvers for heat transfer problems (natural and forced convection), if you can't use the Boussinesq-Approximation. They can be used in cases of large density variation and the can take the compressibility into account.

I would take a look at the maximum expected relative density change in your case. If it is small I would use the boussinesq Solvers -> buoyantBoussinesqSimpleFoam (believing you have an steady state case)

If the Boussinesq-Approximation is not valid in your case, you will have to use buoyantSimpleFoam.

Bye RMF

Aylalisa

[RMF]

Hi Aylalisa,

don't worry about asking me again...it just means that I didn't explain it well ;-)

Let's take a look at an example:

A hot vertical square plate with a length of 0.5 m is heatet up to 225°C. Air with 20 m/s an 25°C flows over the plate.

Let's calculate the different dimensionless numbers

- the density variation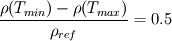

- the Grashof-Number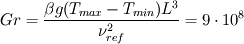

- Reynolds Number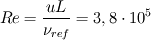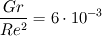

-

So in this case your temperature difference is quiet large. At least it results in a relative density change of 50 %. I wouldn't use the Boussinesq approximation in this case. The fraction of Reynolds^2 and Grashof give you an idea about the major effects in the flow. You can see that the forces caused by the forced convection are dominant. So if you do a calculation and neglect the buoyant effects (by using rhoSimpleFoam) and compare it to a simulation performed with buoyantSimpleFoam, you shouldn't see a difference (if my short calculation is right ;-))

So you can image some cases where you can't use the Boussinesq-Approximation, because of large temperature differences. But the forced convection is dominant, so you can neglect buoyant effects.

Bye RMF

[aylalisa]

Hi RMF,

Originally Posted by RMF

Hi Aylalisa,

don't worry about asking me again...it just means that I didn't explain it well ;-)

It is probably not possible to give a more charming reply to my, kind of inchoate, questions ! I've spent some time on reading. Your answers and that little reading helped me to improve the situation but as well revealed all the complexity of the simulation case.

Originally Posted by RMF

Let's take a look at an example:

A hot vertical square plate with a length of 0.5 m is heatet up to 225°C. Air with 20 m/s an 25°C flows over the plate.

Let's calculate the different dimensionless numbers

- the density variation

- the Grashof-Number

- Reynolds Number

-

How did you determine the thermal expansion coefficient?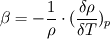



To get the value, did you assume 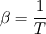, for an ideal gas???

O.k., I see the result of the ratio 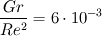but I am not entirely able to classify it.

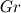With help of I can rate the character of a forced flow and is it's equivalent for natural convection. Do you say that the denominator is dominant and therefore the forces caused by the forced flow are dominant?

Does it mean that if I would suppose a much smaller density change I could use one of the Boussinesq solvers but not the rhoSimpleFoam solver?

Why appears the 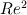number up to the power of 2?
Is that an official ratio? Could you maybe recommend literature that deepens that matter?

Originally Posted by RMF

So in this case your temperature difference is quiet large. At least it results in a relative density change of 50 %. I wouldn't use the Boussinesq approximation in this case. The fraction of Reynolds^2 and Grashof give you an idea about the major effects in the flow. You can see that the forces caused by the forced convection are dominant. So if you do a calculation and neglect the buoyant effects (by using rhoSimpleFoam) and compare it to a simulation performed with buoyantSimpleFoam, you shouldn't see a difference (if my short calculation is right ;-))

So you can image some cases where you can't use the Boussinesq-Approximation, because of large temperature differences. But the forced convection is dominant, so you can neglect buoyant effects.

Bye RMF

I spent more time to think about the case I want to compute and came up with a new choice according to the solver I should use: buoyantBoussinesqPimpleFoam.
There is a forced flow through the duct (fluid: water). I suppose a laminar flow of the fluid. The thermal energy is lead to the fluid through the bottom of the duct. To get buoyant effects in the fluid the T-difference is quite small.
I would like to see the formation of the flow structure that will hopefully arise due to that density changes.
So in that case I would like to analyse the interaction between a forced laminar flow and buoyancy.
Could you give me a recommendation which solver I should use???

And there is still one more question.
I've checked the OpenFoam example cases in the tutorial folder 'heatTransfer'.
I the directory 'buoyantBoussinesqSimpleFoam/iglooWithFridges/0' are listed up the relevant field variables. I have a problem with 'p' and 'p_rgh'. I thought these variables would stand for pressure fields but the dimensions have totally confused me.
for example:
p [0 2 -2 0 0 0 0] -->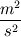
It seems as if the pressure is divided by the density .

With your first answers you gave me an inch and now I will try to take a mile. Anyway I hope for your response!

Aylalisa

[RMF]

Hi,

at the moment I'm quiet busy, so I need to make it short.

How did you determine the thermal expansion coefficient?



To get the value, did you assume , for an ideal gas???

You're completly right!

With help of I can rate the character of a forced flow and is it's equivalent for natural convection. Do you say that the denominator is dominant and therefore the forces caused by the forced flow are dominant?

Yes, you got it ;-)

Why appears the number up to the power of 2?
Is that an official ratio? Could you maybe recommend literature that deepens that matter?

It's a result from the physics. When you non-dimensionalize your Navier-Stokes equation including the buoyancy forces, this ration appears in front of the buyoant term.
The non-dimensionalizing is done here
http://www.cfd-online.com/Forums/mai...tml#post333066
Unfortunately it's only done for the Navier-Stokes equation with constant density. So you can't see the Gr/Re^2 there. But if you do it with the buoyant term, this ratio would appear in front of the term, like the 1/Re in front of the viscous term (this is the reason why for large Re you can use the potential flow field as a far field solution; for Re-> infinity the viscous term disappears in the non-dimensionalized velocity equation).
Maybe I'll find the time to write down these equations in the near future ...

Sorry, all the literature I know and have is in german, so it won't help you...
Actually I did not find to much about the non-dimensionalized Navier-Stokes-Equation for buoyant flows. I learned most of the similarity stuff at university and started to do it for buoyant flows, too.

Could you give me a recommendation which solver I should use???

I would take buoyantBoussinesqSimpleFoam as long as you're not interested in the unsteady developement of the flow. A lot of buoyant flows do not have a steady solution, so if your calculation does not converge you need do take the buoyantBoussinesqPimpleFoam, but I would start with simple.

It seems as if the pressure is divided by the density .

Yeah, that's right. It is quiet common to do that. If you do that, the density does not appear in your Navier-Stokes equations explicitly.

Bye Robert