 |
|
|
[Sponsors] | |||||
How can temperature e treated as a passive scalar be used in transport equation? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Mandeep Shetty
Join Date: Apr 2016
Posts: 185
Rep Power: 10  |
Hello,
Temperature is not a conserved quantity. Then how can temperature be treated as a passive scalar and used in a scalar transport equation? Looking at the transport equation for Temperature it seems to be the same as the energy equation but used for an incompressible isotropic flow independent of temperature. So, is the 'Temperature scalar transport same as energy transport equation? Also, in OpenFOAM when reading about the energy equation I came across internal energy and enthalpy dependent energy equation (HEqn) but the temperature transport equation (TEqn) is not mentioned here. So why is the temperature transport equation not recognized as an Energy equation? |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Mohamed Zayed
Join Date: Sep 2020
Posts: 5
Rep Power: 5  |
There is only the energy conservation equation, originaly expressed in the internal energy and enthalpy terms in its non simplified form http://cadfamily.blogspot.com/2014/1...-transfer.html , it is just in case of incompressible flows can be simplified and considered as the known passive scalar temperature equation to solve for the temperature field.
For incompressible flow you need the "Mass conservation" and "Momentum conservation" to solve the field (that is why in the OpenFOAM incompressible solvers you don't find EEqn files), and the Temperature equation is an independet solved equation (if you add it to the solver as a passive scalar) depending on its thermal diffusivity coefficient, as the velocity and pressure field is already known from the solved coupled Mass and Momentum equations. But for compressible flows the density is changing and so you need an additional equaitons to to solve the field, so the "Energy conservation" and the "state equation" have to be added in the solver to close the set of equations. But this time you have to consider the non simplified form of the energy equation as the internal energy is not only dependent on the temperature anymore. I hope it helped. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Mandeep Shetty
Join Date: Apr 2016
Posts: 185
Rep Power: 10  |
Quote:
|
||
|
|

|
||
|
|
|
#4 |
|
New Member
Mohamed Zayed
Join Date: Sep 2020
Posts: 5
Rep Power: 5  |
I totally agree with you. There is confusion with using temperature instead of energy for the equation naming, but the energy is the quantity conserved in all cases. I think this confusion arises from the fact that the energy equation solves for temperature field.
I will write energy equations for compressible and incompressible flows for future reference. compressible: 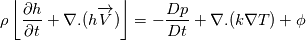 incompressible: 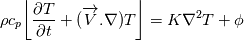 Also, the following document represents the upper equations and the reasons behind the simplification of the equation in the incompressible case clearly: http://users.metu.edu.tr/csert/me582...%20Ch%2001.pdf |
|
|
|

|
|
 |
| Tags |
| energy equation, transport equation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Temperature calculation from total enthalpy in OpenFOAM (XiFOAM) | sharifi | OpenFOAM Running, Solving & CFD | 1 | October 8, 2020 09:16 |
| Adding a scalar transport equation to twoPhaseEulerFoam | shanvach | OpenFOAM Running, Solving & CFD | 1 | October 29, 2018 04:17 |
| problem during mpi in server: expected Scalar, found on line 0 the word 'nan' | muth | OpenFOAM Running, Solving & CFD | 3 | August 27, 2018 04:18 |
| Ansys CFX problem: unexpected very high temperatures in premix laminar combustion | faizan_habib7 | CFX | 4 | February 1, 2016 17:00 |
| transport equation for SGS scalar variance | chinthakindi | Main CFD Forum | 0 | April 27, 2004 09:26 |