In order to build a solver for
 

In order to build a solver for combustion I need to discretize the radiative transfer equation.
The RTE contains the term:

s*grad(I)

where I is a scalar and s a vector.
My problem comes from the gradient operator for which is avaible only the explicit representation but I need an implicit form to solve for I.
So I have thought to use some math and rewrite it in a form containg operator having an implicit discretization such as divergence:

s*grad(I)=div(s*I)-I*div(s)

Should it work?

Yep, looks correct, should wor
 

Yep, looks correct, should work.

surfaceScalarField sf = fvc::surfaceInterpolate(s)& mesh.Sf();
& mesh.Sf()
s * grad(I) := fvm::div(sf, I) - fvm::Sp(fvc::div(fs), I);

the 'Sp' - thing adds a coefficient to the diagonal of the implicit matrix.

Taking this opportunity, why is there no implicit grad implementation? Anybody?

pierre and markus

ignore second & mesh.Sf()
 

ignore second & mesh.Sf()

P & M

Implicit gradient operator:
 

Implicit gradient operator:

- firstly, the diagonal would be zero.
- secondly, the matrix coefficients would be vectors for a gradient and vectors transpose for a divergence
- thirdly, you cannot solve the equation

grad(thingy) = rhs

beucase the diagonal of the gradient matrix equals zero for a uniform mesh

Implicit gradient matrix makes sense only for implicit block coupled (e.g. pressure velocity) algorithms, and I'm pretty sure noone is quite there yet with OpenFOAM.

Hrv

The equation I need to discret
 

The equation I need to discretize is not

s*grad(I)=div(s*I)-I*div(s)

but it contains the "s*grad(I)" that I have thought to sobstitute it with "div(s*I)-I*div(s)".

Hrv, thanks, does make sense.
 

Hrv, thanks, does make sense.

Diego, we decribed the implementation of "s*grad(I)" as "div(s*I)-I*div(s)", which would be one of the terms for the matrix setup (:= means defined as)

fvScalarMatrix yourEqn
(
...
+ fvm::div(sf, I) - fvm::Sp(fvc::div(fs), I)
...
);

PM

Ok thanks so it seems it c
 

Ok thanks

so it seems it could not work.

yes, it can you can't have
 

yes, it can

you can't have the term "s*grad(I)" implicitly, but you can replace that with the term you suggested "div(s*I)-I*div(s)", for which we gave the actual implementation.
The "fvm::"-prefix means in Foam-speak implicit. More precise, it is the "fvm" namespace in which all implicit functions for the Finite Volume Method (fvm) are defined.

"fvc::" denotes "Finite Volume Calculus", all explicit stuff.

So again, your reasoning is right, you can do it as you suggested.

P & M

Sorry but I did not get what J
 

Sorry but I did not get what Jasak was writing so I guessed it would not have worked.

Thank you again.

Hi Diego, I think that "s"
 

Hi Diego,

I think that "s" is a const vector, once u have decided the direction of the radiation...
so div(s) must be equal to zero.

So, I think u can write:
s&grad(I) = div(sI)

bye
M

Hi This might be a dumb que
 

Hi

This might be a dumb question but is this why the pressure is solved in a semi-discretised form of the momentum equation (A and H decompositions and solving through Jacobi metod) i.e. to find another way of implementing an implicit form of grad(p)?

/Erik

Do you know CFX? They impleme
 

Do you know CFX? They implement a pressure-based block solver and they indeed have an implicit grad (and div!) to form a 2x2 block matrix system.

No such thing in OpenFOAM at the moment.

Hrv

Thank you Hrv! I guess this
 

Thank you Hrv!

I guess this is the reason for the special treatment of grad(p) then.

I dont know about CFX. I am fairly new to the field of CFD and keen on using and learning more about OpenFOAM.

My problem is that I am trying to implement a different momentum equation involving gradients of density as well as the gradient of pressure. I would like to know how to formulate this in a similar manner to the one done in the PISO-loop. Ive looked through your Ph.D and found some information on the subject but I would like to see some DOC (if available) on how to get the momentum equation in the semi-discretised form. Is such DOC available to your knowledge?

regards
/Erik

Hello, could anyone explain these arguments more detailed?

Thanks

Even if it has passed quite a few time since this post I'll answer anyway.

If you discretize your gradient with a finite Volume Method and sum the values over the faces of your control volume, the value at your control volume center cancels out for a regular grid.

I came across the same problem after discretizing of the gradient of an scalar.

The gradient of a scalar is discretized as



Where the lower f indicates the value of the scalar at the faces



F represents the neighboring nodes

For an weight of 0.5



So the gradient can be written as



For a structured grid we can assume that the normal vector of one face must be the normal vector of another face just in the opposite direction



We can see that in the discretized form the center point of the owner vanishes



The obtained matrix wont have any diagonal elements.

I stumbled across this thread while searching for a way to discretize a somehow similar problem. I need to discretize the following term:

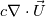Rearranging the divergence term: 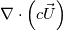gives results in the following discretization:

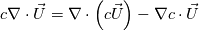The implementation of the first term of the RHS should be:
Based on the example above, I've tried to implement the second term of the RHS as follows:
However, the second term doesn't compile, since there is no suitable Sp method available for the supplied arguments. I'm missing something on this term.

Has anybody of you an idea on how to correctly discretize RHS?

Hello mboesi,


did you already solve your problem?


I'm facing the same issue.


With kind regards
Christian

I think here the problem is that phi is a surfaceScajarfield and not a volScalarField. The second argument of the fvm:: Sp operator should always be the variable you are solving for and the variables are defined at the cell centers. The OpenFOAM propramer guide gives some advice how to use it

has anybody solved this problem？