CFD Online Discussion Forums - modify laplacian: div(k*grad(a*u))

CFD Online Discussion Forums (https://www.cfd-online.com/Forums/)

- OpenFOAM Running, Solving & CFD (https://www.cfd-online.com/Forums/openfoam-solving/)

- - modify laplacian: div(k*grad(a*u)) (https://www.cfd-online.com/Forums/openfoam-solving/91282-modify-laplacian-div-k-grad-u.html)

gunnar2

August 5, 2011 11:42

modify laplacian: div(k*grad(a*u))

Hello,
I am trying to solve a type of heat equation:

$\partial u/ \partial t + \nabla\cdot\mathbf{v} u - \nabla\cdot k \nabla \alpha u =0$

The difference to the standard heat equation is the scalar field alpha.
The problem is that the last term cannot be expressed as fvm::laplacian(k,alpha*u), because apparently alpha*u is not the right class for this argument, and the compiler fails.

How can this PDE be solved?

Thanks
Gunnar

ata	August 6, 2011 05:00

Hi
I think you can define a new field newfield=alpha*u and use fvc::laplacian(k,new)
good luck

gunnar2

August 6, 2011 06:11

But I need the implicit (fvm::laplacian), not the explicit (fvc::laplacian) term.

If there is no such term, it should be possible to use something like fvm::laplacian(k,u)*diag(alpha) for 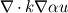$\nabla\cdot k\nabla \alpha u$ .
diag(alpha) would be a sparse diagonal matrix with the entries of the field alpha on it's diagonal, but I don't think such matrix exists in Openfoam.
What do you think, does it make sense to implement it?

Thanks
Gunnar

ata	August 7, 2011 05:10

Hi
I do not know:(

roth	August 7, 2011 11:42

How about a little chain rule? i.e. split into:

Code:

\nabla \cdot ( k \alpha \nabla u ) + \nabla \cdot ( k u \nabla \alpha )

Then treat the first term implicit (by defining a new diffusivity of k\alpha) and second term explicit.

ata	August 7, 2011 12:29

Hi
But you loose conservative form.

santiagomarquezd

August 8, 2011 08:43

First of all the equation appears to be not consistent, the first and last terms are vectorial, meanwhile the second one is scalar.

Regards.

ziemowitzima

August 21, 2011 14:53

Hi Gunnar,
If the only think you need is modification of the discretization matrix (by multiplying diag(alpha)), then you can change the matrix itself.
See the PISO algorithm from icoFoam:
http://openfoamwiki.net/index.php/IcoFoam
You can do similar and:
1. discretize alpha
2. UEqn.A() = UEqn.A()*alpha_discretized

maybe will work...
ZMM

kaifu

August 21, 2011 16:44

$\nabla\cdot (k \nabla \alpha \mathbf{u}) =\nabla \cdot (k\alpha\nabla \mathbf{u})+\nabla\cdot (k \mathbf{u} \nabla \alpha)=\nabla \cdot (k\alpha\nabla \mathbf{u})+(\nabla \cdot k \mathbf{u})\nabla \alpha$

ziemowitzima

August 21, 2011 17:36

Hi Kai,
Of course,
I would proceed using this transformation.
Currently I have some issues with laplacian operator in OFoam as well.
Could you see my post:
http://www.cfd-online.com/Forums/ope...n-problem.html

Maybe you will have some suggestions...
Thanks
ZMM

All times are GMT -4. The time now is 13:14.