CFD Online Discussion Forums

CFD Online Discussion Forums (https://www.cfd-online.com/Forums/)
-   OpenFOAM (https://www.cfd-online.com/Forums/openfoam/)
-   -   Implementing an Equation (https://www.cfd-online.com/Forums/openfoam/113993-implementing-equation.html)

Yahoo March 3, 2013 00:25
Implementing an Equation
 
Hi FOAMERS

Do you know the simplest way to implement equation "dC/dt + grad(CL).V = 0", where C and CL are scalar and V is the velocity vector?

chegdan March 3, 2013 16:02
This could be done as

Code:
fvScalarMatrix CEqn
(
      fvm::ddt(C)
    + U & fvc::grad(CL)
);

CEqn.solve();
But the two variables C and CL are going to be explicitly coupled since grad is explicit. If in fact CL was actually some other variable related to C, say C+C0 then you could be more clever and do something like

Code:
fvScalarMatrix CEqn
(
      fvm::ddt(C)
    + fvm::div(phi,C)
    + fvm::SuSp(-fvc::div(phi),C)
    + U & fvc::grad(C0)
);

CEqn.solve();
where this is a more conservative form of your original equation, that of course will work if CL is actually C plus something else. I'm not sure what you are working on....so I'm just throwing things out there at this point :D.

Yahoo March 5, 2013 12:44
Daniel
Thanks for your answer.

In my case C = (gL + kp*(1-gL))CL, where gL is a volScalaerField and kp is constant. You have any ideas of the best way to implement this?

By the way, can you explain why adding term "fvm::SuSp(-fvc::div(phi),C)" makes it more conservative?

chegdan March 5, 2013 13:33
Quote:
By the way, can you explain why adding term "fvm::SuSp(-fvc::div(phi),C)" makes it more conservative?
The conservative (strong) form of the advection operator is

\qquad\nabla\cdot\left(\vec{U}C\right)=\vec{U}\cdot\nabla C + C\left(\nabla\cdot\vec{U}\right)

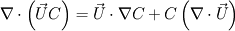the

Code:
fvm::SuSp(-fvc::div(phi),C)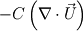
is just

- C\left(\nabla\cdot\vec{U}\right)

If there is incomplete convergence in your momentum portion of your solver, this will account for that fact. For a completely converged velocity field, this term will approach zero for an incompressible fluid (i.e. by the nature of continuity). Take a look at the thread http://www.cfd-online.com/Forums/ope...silon-eqn.html and the post http://www.cfd-online.com/Forums/ope...tml#post280210. This is also implemented in the k-epsilon turbulence models if you would like to look at them.

anishtain4 March 6, 2013 01:35
Dear chegdan,

I believe the left side of your equation is conservative form, the right side is called primitive form. The reason for the name comes from gas dynamics and passing through the shocks. When you use the left hand side (consider C as as rho) passing through the shock your momentum will remain constant, however on your right hand side every term experiences a severe gradient which makes numerical instabilities in presence of shock.
PS: I'm speaking in the context of gas dynamics, please let me know if I'm wrong.

chegdan March 12, 2013 12:08
Quote:
I believe the left side of your equation is conservative form, the right side is called primitive form. The reason for the name comes from gas dynamics and passing through the shocks. When you use the left hand side (consider C as as rho) passing through the shock your momentum will remain constant, however on your right hand side every term experiences a severe gradient which makes numerical instabilities in presence of shock.
Thanks! Nice to learn some new lingo.


All times are GMT -4. The time now is 11:07.