 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 615
Rep Power: 15  |
The rotate function in the file \$FOAM_SRC/sixDoFRigidBodyMotion/sixDoFRigidBodyMotion/sixDoFRigidBodyMotionI.H
looks as follows: Code:
inline Foam::Tuple2<Foam::tensor, Foam::vector>
Foam::sixDoFRigidBodyMotion::rotate
(
const tensor& Q0,
const vector& pi0,
const scalar deltaT
) const
{
Tuple2<tensor, vector> Qpi(Q0, pi0);
tensor& Q = Qpi.first();
vector& pi = Qpi.second();
tensor R = rotationTensorX(0.5*deltaT*pi.x()/momentOfInertia_.xx());
pi = pi & R;
Q = Q & R;
R = rotationTensorY(0.5*deltaT*pi.y()/momentOfInertia_.yy());
pi = pi & R;
Q = Q & R;
R = rotationTensorZ(deltaT*pi.z()/momentOfInertia_.zz());
pi = pi & R;
Q = Q & R;
R = rotationTensorY(0.5*deltaT*pi.y()/momentOfInertia_.yy());
pi = pi & R;
Q = Q & R;
R = rotationTensorX(0.5*deltaT*pi.x()/momentOfInertia_.xx());
pi = pi & R;
Q = Q & R;
return Qpi;
}
What i figured out so fare the intention of this function is to compute the angle difference between the local coordinate system at the old and new time step. For this purpose one can use the equation for the angular momentum L 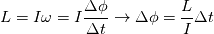 Beeing I the diagonal inertial tensor and phi a vector. So my question is why the function first rotates half angle around the first axis, then half angle around the second axis, the full angle around the third axis, than half angle around the second axis and half angle around the first axis. What is the difference to perform the full rotation around the first, second and third axis? Best Michael |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 615
Rep Power: 15  |
Maybe some additional background:
What I found so far is that in OpenFoam (I checked 2006) to obtain the new orientation of the local body fixed coordinate system we first integrate the equation of motion for the angular momentum transformed to the local coordinate system: 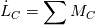 The subscript C denotes that the angular momentum is computed using the center of gravity as reference point. If we integrate this equation ones we get the angular momentum at the new time step 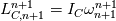 The moment of inertia in the above equation is only diagonal if axis of the local coordinate system are aligned with the axis of inertia. The subcript n+1 denotes that the vectors are expressed in the local coordinate system at the time step n+1 and the superscript n+1 denotes the time step at which the solution is computed. Unfortunately we know only the orientation of the local coordinate system in the last time step n. We get a first order approximation of the above equation if we express the vectors in the local coordinate system at the time step n: 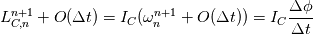 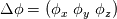 is the vector of angle differences between the orientation of the axis of the local coordinate system at the time step n and n+1. is the vector of angle differences between the orientation of the axis of the local coordinate system at the time step n and n+1.So if we rotate the axis of the local coordinate system by the three angles increments 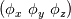 we get the orientation of the local coordinate system at the new time step. we get the orientation of the local coordinate system at the new time step. What i do not understand is why the rotate function is constructed like described in the previous post. Last edited by mAlletto; August 10, 2020 at 10:49. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [mesh manipulation] RefineMesh Error and Foam warning | jiahui_93 | OpenFOAM Meshing & Mesh Conversion | 4 | March 3, 2018 11:32 |
| [blockMesh] error message with modeling a cube with a hold at the center | hsingtzu | OpenFOAM Meshing & Mesh Conversion | 2 | March 14, 2012 09:56 |
| ParaView for OF-1.6-ext | Chrisi1984 | OpenFOAM Installation | 0 | December 31, 2010 06:42 |
| Compilation errors in ThirdPartymallochoard | feng_w | OpenFOAM Installation | 1 | January 25, 2009 06:59 |
| Problem with compile the setParabolicInlet | ivanyao | OpenFOAM Running, Solving & CFD | 6 | September 5, 2008 20:50 |