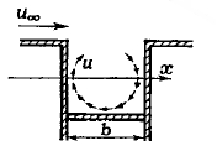
2-D laminar/turbulent driven square cavity flow
From CFD-Wiki
Introduction
A classical test problem is numerical simulation of a laminar/turbulent flow of an incompressible viscous fluid in a square cavity with the upper moving boundary. It has long since been a "testing area" for approbation of approximation schemes for terms in initial equations as well as of computational models and methods. A large number of calculation data concerning this problem have been accumulated. Therefore, it makes sense to return periodically to the solution of the problem verification and analysis of the computational codes developed.
History
The problem of a circulation flow in a cavity is of interest because of the relatively low level of computational resources required for its solution. In this case, the control volume is limited. Therefore, a small number of grid nodes are required and simple boundary conditions are set.{{fact} In the earliest renditions of this problem, the Navier–Stokes equations were transformed into vorticity–stream function variables for economy of computational resources. were obtained. The calculations were performed by brigades of specialists without the use of computers.
When computers appeared, the indicated problem remained, as before, the focus of attention of specialists developing computational methods. A detailed analysis of methods concerning the problem considered that appeared in the period from the 1960s to the late 1980s is given in a set of monographs (for example 1, 2, 3). One of the first works in the area of numerical investigation of a viscous-fluid flow in a square cavity began thirty years ago [1] on a BESM-4 computer containing 21 × 21 grid nodes in one memory cube. At that time, in the mid-1970s, high-accuracy Arakava schemes of the second and fourth order of approximation and nonuniform grids were used for the first time for solving Navier–Stokes equations.
One of the most important scientific achievements of the CFD in the 1980's was a numerical solution of the diffusion problem, since this problem is associated with errors in approximation of convective terms of equations. In simulation of separation flows, a necessary condition for obtaining an exact result is the use of schemes with a low numerical viscosity (upwind schemes of the second and higher orders of approximation of the type of the Leonard scheme with quadratic interpolation, the Agarval scheme, and others) for representation of convective terms in transfer equations. At the same time, it has been established that the first-order schemes give erroneous solutions at high Reynolds numbers even in the case where multi-grid methods are used.
Progress in computational engineering and, especially, widespread use of personal computers in the 1980's and subsequent years have made it possible, first of all, to develop universal first-wave codes of applied programs, such as PHOENIX, FLOW3D, and FIDAP, and then more modern information products / commercial CFD codes such as FLUENT, StarCD, and CFX. When computers with a large memory and a high CPU speed appeared, instead of the Navier–Stokes equations in transformed variables, Navier–Stokes equations written in physical variables — Cartesian velocity or pressure components — began to be predominantly used. This made it possible to increase the number of computational cells (by an order of magnitude and more) and to increase the resolution in the near-wall region for this problem.
Referemces
[1] Isaev S. A., Baranov P. A., Kudryavtsev N. A., Lysenko D. A., and Usachov A. E. SIMULATION OF A CIRCULATION LAMINAR FLOW AROUND A SQUARE CAVITY WITH A MOBILE BOUNDARY AT HIGH REYNOLDS NUMBERS WITH THE USE OF VP2/3 AND THE FLUENT PACKAGE. Journal of Engineering Physics and Thermophysics, Vol. 78, No. 4, 2005
[2] Isaev S. A., Baranov P. A., Kudryavtsev N. A., Lysenko D. A., and Usachov A. E. Complex Analysis of turbulence models, algorithms, and grid structures at the computation of recirculating flow in a cavity by means of VP2/3 and FLUENT packages. Part 1. Scheme factors influence. Thermophysics and Aeromechanics, 2005, Vol: 12, No 4.
[3] Isaev S. A., Baranov P. A., Kudryavtsev N. A., Lysenko D. A., and Usachov A. E. Complex Analysis of turbulence models, algorithms, and grid structures at the computation of recirculating flow in a cavity by means of VP2/3 and FLUENT packages. Part 2. Estimation of models adequacy. Thermophysics and Aeromechanics, 2006 , Vol 13, No 1.