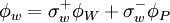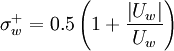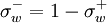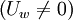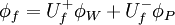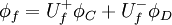Approximation Schemes for convective term - structured grids - definitions
From CFD-Wiki
(→node stencil) |
|||
| (25 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | == Goals of this section == | |
| - | * in different | + | Here we shall develop a commone definitions and regulations because of |
| + | |||
| + | * in different issues was used different definitions and notations | ||
* we are searching for common approach and generalisation | * we are searching for common approach and generalisation | ||
| - | == Usual | + | '''Please note:''' ''as we still developing this section, you can find the rest of non-unificated definitions'' |
| + | |||
| + | == Usual used definition for convected variable == | ||
<math> | <math> | ||
| Line 12: | Line 16: | ||
<math> | <math> | ||
\boldsymbol{\phi} | \boldsymbol{\phi} | ||
| - | </math> | + | </math> |
| + | |||
| + | we shall use here <math>\boldsymbol{\phi}</math> | ||
== definition of considered face, upon wich approximation is applied == | == definition of considered face, upon wich approximation is applied == | ||
| - | usually | + | usually (in the most articles) west face <math> |
| + | \boldsymbol{w} </math> of the control volume is considered ''without loss of generality'' | ||
| - | <math> | + | for which '''flux is directed from the left to the right''' i.e. <math> \boldsymbol{U_{f} \triangleright 0 } </math> |
| - | \boldsymbol{w} | + | |
| - | </math> | + | |
| + | we shall define it as <math> \boldsymbol{f} </math> | ||
| + | |||
| + | and convected variable at face of CV as <math> \boldsymbol{\phi_{f}} </math> | ||
| + | |||
| + | |||
| + | also you can find in literature such definition as <math> \boldsymbol{i+1/2} </math> , but we suggested it non suitable, because of complication | ||
| + | |||
| + | == indicators of the local velocity direction == | ||
| + | |||
| + | approximation scheme can be written in the next form | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | \phi_{w}=\sigma^{+}_{w}\phi_{W} + \sigma^{-}_{w}\phi_{P} | ||
| + | </math> | ||
| + | </td><td width="5%">(1)</td></tr></table> | ||
| + | |||
| + | |||
| + | where <math>\sigma^{+}_{w}</math> and <math>\sigma^{-}_{w}</math> are the indicators of the local velocity direction such that | ||
| + | |||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | \sigma^{+}_{w} = 0.5 \left( 1 + \frac{\left|U_{w} \right|}{U_{w}} \right) | ||
| + | </math> | ||
| + | </td><td width="5%">(1)</td></tr></table> | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | \sigma^{-}_{w} = 1 - \sigma^{+}_{w} | ||
| + | </math> | ||
| + | </td><td width="5%">(1)</td></tr></table> | ||
| + | |||
| + | and of course | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | <math> | ||
| + | \left( U_{w} \neq 0 \right) | ||
| + | </math> | ||
| + | </td><td width="5%">(1)</td></tr></table> | ||
| + | |||
| + | also used such definitions as <math>U^{+}_{w}</math> and <math>U^{-}_{w}</math> | ||
| + | |||
| + | we offer to use | ||
| + | |||
| + | <math>U^{+}_{f}</math> and <math>U^{-}_{f}</math> | ||
| + | |||
| + | therefore unnormalised form of approximation scheme can be written | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | <math> | ||
| + | \phi_{f}=U^{+}_{f}\phi_{W} + U^{-}_{f}\phi_{P} | ||
| + | </math> | ||
| + | </td><td width="5%">(1)</td></tr></table> | ||
| + | |||
| + | or in more general form | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | <math> | ||
| + | \phi_{f}=U^{+}_{f}\phi_{C} + U^{-}_{f}\phi_{D} | ||
| + | </math> | ||
| + | </td><td width="5%">(1)</td></tr></table> | ||
| + | |||
| + | == definitions for NV diagram == | ||
| + | |||
| + | |||
| + | we discovered such definitions as | ||
| + | |||
| + | <math>\boldsymbol{ \hat{\phi}_{i+1/2} }</math> is a function of <math>\boldsymbol{ \hat{\phi}_{i}} </math> | ||
| + | |||
| + | <math>\boldsymbol{ \hat{\phi_{w}} }</math> is a function of <math>\boldsymbol{ \hat{\phi}_{W}} </math> | ||
| + | |||
| + | we shall use here | ||
| + | |||
| + | <math>\boldsymbol{ \hat{\phi_{f}} }</math> is a function of <math>\boldsymbol{ \hat{\phi}_{C}} </math> | ||
| + | |||
| + | == node stencil == | ||
| + | |||
| + | Bear in mind this stencil | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
| - | + | <i> Return to [[Approximation Schemes for convective term - structured grids]] </i> | |
Latest revision as of 01:14, 9 November 2005
Contents |
Goals of this section
Here we shall develop a commone definitions and regulations because of
- in different issues was used different definitions and notations
- we are searching for common approach and generalisation
Please note: as we still developing this section, you can find the rest of non-unificated definitions
Usual used definition for convected variable
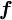
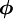
we shall use here 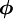
definition of considered face, upon wich approximation is applied
usually (in the most articles) west face 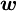 of the control volume is considered without loss of generality
of the control volume is considered without loss of generality
for which flux is directed from the left to the right i.e. 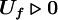
we shall define it as 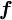
and convected variable at face of CV as 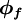
also you can find in literature such definition as 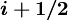 , but we suggested it non suitable, because of complication
, but we suggested it non suitable, because of complication
indicators of the local velocity direction
approximation scheme can be written in the next form
|
| (1) |
where 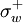 and
and 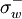 are the indicators of the local velocity direction such that
are the indicators of the local velocity direction such that
|
| (1) |
|
| (1) |
and of course
|
| (1) |
also used such definitions as 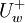 and
and 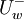
we offer to use
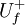 and
and 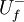
therefore unnormalised form of approximation scheme can be written
|
| (1) |
or in more general form
|
| (1) |
definitions for NV diagram
we discovered such definitions as
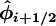 is a function of
is a function of 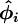
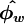 is a function of
is a function of 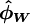
we shall use here
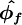 is a function of
is a function of 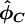
node stencil
Bear in mind this stencil
Return to Numerical Methods
Return to Approximation Schemes for convective term - structured grids