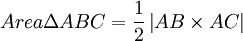Area calculations
From CFD-Wiki
(Difference between revisions)
RoletOchic (Talk | contribs) m (getcnac) |
m (Reverted edits by RoletOchic (Talk) to last version by Zxaar) |
||
| Line 1: | Line 1: | ||
| - | |||
== Area of Triangle == | == Area of Triangle == | ||
<p>The area of a triangle made up of three vertices '''A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3)''' can be represented <br>by the vector-cross-product of vectors along two sides of the triangle sharing a common vertex. <br>For the above mentioned triangle we have three sides as '''AB''', '''BC''' and '''CA''', the area of triangle is given by:<br> | <p>The area of a triangle made up of three vertices '''A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3)''' can be represented <br>by the vector-cross-product of vectors along two sides of the triangle sharing a common vertex. <br>For the above mentioned triangle we have three sides as '''AB''', '''BC''' and '''CA''', the area of triangle is given by:<br> | ||
Latest revision as of 12:31, 19 December 2008
Area of Triangle
The area of a triangle made up of three vertices A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3) can be represented
by the vector-cross-product of vectors along two sides of the triangle sharing a common vertex.
For the above mentioned triangle we have three sides as AB, BC and CA, the area of triangle is given by:
AC = Vector from vertex A to vertex C.
Area of Polygonal Surface
A polygon can be divided into triangles sharing a common vertex of the polygon. The total area of the polygon
can be approximated by sum of all triangle-areas it is made up of.
Return to Numerical Methods