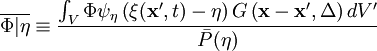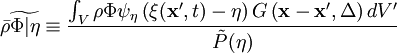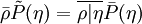Conditional filtering
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 11: | Line 11: | ||
The probability density function | The probability density function | ||
<math>\bar{P}(\eta) </math> is a [[subgrid PDF]] and <math> \eta </math> is the sample space of the passive scalar | <math>\bar{P}(\eta) </math> is a [[subgrid PDF]] and <math> \eta </math> is the sample space of the passive scalar | ||
| - | <math> \xi </math>. In variable density flows, conditional density-weighted | + | <math> \xi </math>. |
| - | (Favre) filtering is used, | + | In variable density flows, the conditional density-weighted (Favre) filtering is used. |
| - | <math> \bar{\rho} | + | Using the density-weighted PDF , <math> \tilde {P}(\eta) </math>, the conditionally Favre filtered operation is |
| + | |||
| + | :<math> | ||
| + | \bar{\rho} \widetilde{\Phi|\eta} \equiv \frac{\int_V \rho \Phi \psi_\eta \left( | ||
| + | \xi(\mathbf{x'},t) - \eta | ||
| + | \right) G \left( \mathbf{x} -\mathbf{x'}, \Delta \right) dV'}{\tilde {P}(\eta)} | ||
| + | </math> | ||
| + | |||
| + | The relation between Favre and conventional PDF's is | ||
| + | :<math> | ||
| + | \bar{\rho} \tilde{P}(\eta) = \overline{\rho|\eta}\bar{P}(\eta) | ||
| + | </math> | ||
Latest revision as of 12:38, 8 May 2006
A conditional filtering operation of a variable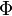 
is defined as
where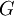 
is a positive defined space filter with filter width 
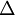(see LES filters),
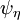is a fine-grained probability density function,
which is taken as a Dirac delta 
.
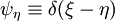The probability density function
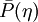is a subgrid PDF and 
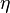is the sample space of the passive scalar
.
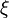In variable density flows, the conditional density-weighted (Favre) filtering is used.
Using the density-weighted PDF ,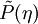 
, the conditionally Favre filtered operation is
The relation between Favre and conventional PDF's is
