Diffusion term
From CFD-Wiki
| Line 43: | Line 43: | ||
== Reference == | == Reference == | ||
| - | #'''Ferziger, J.H. and Peric, M. 2002'''. | + | #'''Ferziger, J.H. and Peric, M. 2002'''. <i>Computational Methods for Fluid Dynamics</i>, 3rd rev. ed., Springer-Verlag, Berlin. |
# '''Jasak Hrvoje''', ''PhD. Thesis'', "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows " | # '''Jasak Hrvoje''', ''PhD. Thesis'', "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows " | ||
Revision as of 06:48, 15 September 2005
Contents |
Discretisation of Diffusive Term
Description
Note: The approaches those are discussed here are applicable to non-orthoganal meshes as well as orthogonal meshes.
A control volume in mesh is made up of set of faces enclosing it. The figure 1.1 shows a typical situation. Where A represent the magnitude of area of the face. And n represents the normal unit vector of the face under consideration.
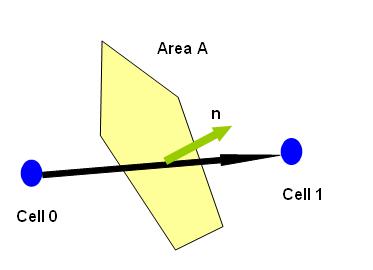
Figure 1.1
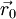 and
and 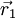 are position vector of centroids of cells cell 0 and cell 1 respectively.
are position vector of centroids of cells cell 0 and cell 1 respectively.
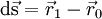
We wish to approaximate 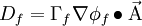 at the face.
at the face.
Approach 1
Another approach is to use a simple expression for estimating the gradient of scalar normal to the face.
where 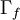 is suitable face averages.
is suitable face averages.
This approach is not very good when the non-orthogonality of the faces increases. Instead for the fairly non-orthogonal meshes, it is advisable to use the following approaches.
Approach 2
We define vector
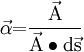
giving us the expression:
where 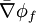 and
and 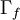 are suitable face averages.
are suitable face averages.
Reference
- Ferziger, J.H. and Peric, M. 2002. Computational Methods for Fluid Dynamics, 3rd rev. ed., Springer-Verlag, Berlin.
- Jasak Hrvoje, PhD. Thesis, "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows "

![D_f = \Gamma _f \nabla \phi _f \bullet \vec A = \Gamma _f \left[ {\left( {\phi _1 - \phi _0 } \right)\left| {{{\vec A} \over {d\vec s}}} \right|} \right]](/W/images/math/e/b/a/eba7a8f962a26ccc4322e8e4cde187ee.png)
![D_f = \Gamma _f \nabla \phi _f \bullet {\rm{\vec A = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _1 - \phi _0 } \right)\vec \alpha \bullet {\rm{\vec A + }}\bar \nabla \phi \bullet {\rm{\vec A - }}\left( {\bar \nabla \phi \bullet {\rm{d\vec s}}} \right)\vec \alpha \bullet {\rm{\vec A}}} \right]](/W/images/math/7/7/2/772b96059e9032fc07b25c0dee76db6c.png)