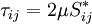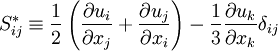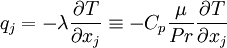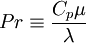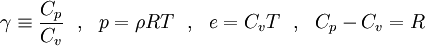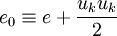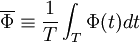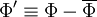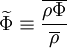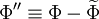Favre averaged Navier-Stokes equations
From CFD-Wiki
Instantaneuos Equations
The instantaneous continuity equation (1), momentum equation (2) and energy equation (3) for a compressible fluid can be written as:
|
| (1) |
|
| (2) |
|
| (3) |
For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous stress is given by:
|
| (4) |
Where the trace-less viscous strain-rate is defined by:
|
| (5) |
The heat-flux, 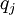 , is given by Fourier's law:
, is given by Fourier's law:
|
| (6) |
Where the laminar Prandtl number 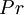 is defined by:
is defined by:
|
| (7) |
To close these equations it is also necessary to specify an equation of state. Assuming a calorically perfect gas the following relations are valid:
|
| (8) |
Where 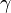 ,
, 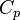 ,
, 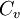 and
and 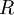 are constant.
are constant.
The total energy 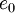 is defined by:
is defined by:
|
| (9) |
| Insert Reference |
Equations (1)-(9), supplemented with gas data for 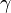 ,
, 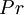 ,
, 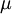 and perhaps
and perhaps 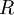 , form a closed set of partial differential equations, and need only be complemented with boundary conditions.
, form a closed set of partial differential equations, and need only be complemented with boundary conditions.
Favre Averaged Equations
It is not possible to solve the instantaneous equations directly for the applications of interest here. At the Reynolds numbers typically present in a turbine these equations have very chaotic turbulent solutions, and it is necessary to model the influence of the smallest scales. All turbulence models used in this work are based on one-point averaging of the instantaneous equations. The averaging procedure used is described in the next sections.
Averaging
Let 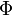 be any dependent variable. It is convenient to define
two different types of averaging of
be any dependent variable. It is convenient to define
two different types of averaging of 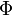 :
:
- Classical time average (Reynolds average):
|
|
(10) |
|
|
- Density weighted time average (Favre average):
|
| (11) |
|
|
Note that with the above definitions 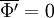 , but
, but 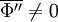 .
.
![\frac{\partial \overline{\rho}}{\partial t} +
\frac{\partial}{\partial x_i}\left[ \overline{\rho} \widetilde{u_i} \right] = 0](/W/images/math/d/c/d/dcd521718edfb790fcf5915dfff51dde.png)
![\frac{\partial}{\partial t}\left( \overline{\rho} \widetilde{u_i} \right) +
\frac{\partial}{\partial x_j}
\left[
\overline{\rho} \widetilde{u_j} \widetilde{u_i}
+ \overline{p} \delta_{ij}
- \widetilde{\tau_{ji}^{tot}}
\right]
= 0](/W/images/math/c/9/f/c9fb98d7716cc9a91f7e78b0ed597728.png)

![\frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0](/W/images/math/0/7/1/071e4f5508fd336ddad848551ce3188e.png)
![\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0](/W/images/math/6/f/c/6fc8041faa4be98ee72ec1e670fb22c7.png)
![\frac{\partial}{\partial t}\left( \rho e_0 \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_j e_0 + u_j p + q_j - u_i \tau_{ij} \right] = 0](/W/images/math/8/1/7/8176cdf87a72617542883cbbeafc50cc.png)