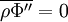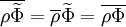Favre averaging
From CFD-Wiki
Let 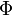 be any dependent variable. This variable can be decomposed into a mean part
be any dependent variable. This variable can be decomposed into a mean part 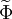 and a fluctuating part
and a fluctuating part 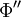 using a density weighted average in the following way:
using a density weighted average in the following way:
|
| |
|
| (1) |
|
where the overbars (e.g. | |
|
auxiliary relations include | |
|
| |
|
|
Favre averaging is sometimes used in compressible flow to separate turbulent fluctuations from the mean-flow. In most cases it is not necessary to use Favre averaging though, since turbulent fluctuations most often do not lead to any signigicant fluctuations in density. In that case the more simple Reynolds averaging can be used. Only in highly compressible flows and hypersonic flows is it necassary to perform the more complex Favre averaging.
Favre averaging can be used to derive the Favre averaged Navier-Stokes equations.

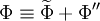
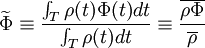
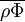 ) denote averages using the Reynolds decomposition.
) denote averages using the Reynolds decomposition.