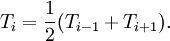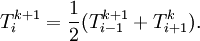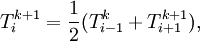Gauss-Seidel method
From CFD-Wiki
(→Example Calculation: Added more data) |
m (→Example Calculation) |
||
| Line 84: | Line 84: | ||
:<math> T_i = \frac{1}{2}(T_{i-1}+T_{i+1}).</math> | :<math> T_i = \frac{1}{2}(T_{i-1}+T_{i+1}).</math> | ||
| - | Then, stepping through the solution vector from <math>i=2</math> to <math>i=n-1</math>, we can compute the next iterate from the two surrounding values. Note that (in this scheme), <math>T_{i+1}</math> is from the previous iteration, while <math>T_{i-1}</math> is from the current iteration. | + | Then, stepping through the solution vector from <math>i=2</math> to <math>i=n-1</math>, we can compute the next iterate from the two surrounding values. Note that (in this scheme), <math>T_{i+1}</math> is from the previous iteration, while <math>T_{i-1}</math> is from the current iteration: |
| + | |||
| + | :<math> T_i^{k+1} = \frac{1}{2}(T_{i-1}^{k+1}+T_{i+1}^k).</math> | ||
| + | |||
| + | The following table gives the results of 10 iterations with 5 nodes (3 interior and 2 boundary) as well as <math>L_2</math> norm error. | ||
{| align=center border=1 | {| align=center border=1 | ||
| Line 179: | Line 183: | ||
|} | |} | ||
| - | In this situation, the direction that we "sweep" is important - if we step though the solution vector in the opposite direction, the solution moves away from the chosen initial condition (zero everywhere in the interior) more quickly. | + | In this situation, the direction that we "sweep" is important - if we step though the solution vector in the opposite direction, the solution moves away from the chosen initial condition (zero everywhere in the interior) more quickly. The iteration is defined by |
| + | |||
| + | :<math> T_i^{k+1} = \frac{1}{2}(T_{i-1}^{k}+T_{i+1}^{k+1}),</math> | ||
| + | |||
| + | and this gives us (slightly) faster convergence, as shown in the table below. | ||
{| align=center border=1 | {| align=center border=1 | ||
Revision as of 07:36, 8 April 2006
Introduction
We seek the solution to set of linear equations:
In matrix terms, the the Gauss-Seidel iteration can be expressed as
where 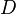 ,
, 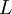 , and
, and 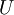 represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix
represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix 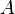 and
and  is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
Note that the computation of 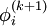 uses only those elements of
uses only those elements of 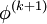 that have already been computed and only those elements of
that have already been computed and only those elements of 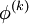 that have yet to be advanced to iteration
that have yet to be advanced to iteration 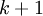 . This means that no additional storage is required, and the computation can be done in place (
. This means that no additional storage is required, and the computation can be done in place (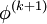 replaces
replaces 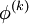 ). While this might seem like a rather minor concern, for large systems it is unlikely that every iteration can be stored. Thus, unlike the Jacobi method, we do not have to do any vector copying should we wish to use only one storage vector. The iteration is generally continued until the changes made by an iteration are below some tolerance.
). While this might seem like a rather minor concern, for large systems it is unlikely that every iteration can be stored. Thus, unlike the Jacobi method, we do not have to do any vector copying should we wish to use only one storage vector. The iteration is generally continued until the changes made by an iteration are below some tolerance.
Algorithm
- Chose an initial guess
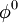
- for k := 1 step 1 until convergence do
- for i := 1 step until n do
-
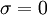
- for j := 1 step until i-1 do
-
- end (j-loop)
- for j := i+1 step until n do
-
- end (j-loop)
-
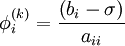
-
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (k-loop)
Example Calculation
In some cases, we need not even explicitly represent the matrix we are solving. Consider the simple heat equation problem
subject to the boundary conditions 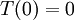 and
and 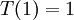 . The exact solution to this problem is
. The exact solution to this problem is 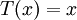 . The standard second-order finite difference discretization is
. The standard second-order finite difference discretization is
where 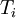 is the (discrete) solution available at uniformly spaced nodes. In matrix terms, this can be written as
is the (discrete) solution available at uniformly spaced nodes. In matrix terms, this can be written as
However, for any given 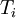 for
for 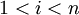 , we can write
, we can write
Then, stepping through the solution vector from 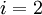 to
to 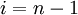 , we can compute the next iterate from the two surrounding values. Note that (in this scheme),
, we can compute the next iterate from the two surrounding values. Note that (in this scheme), 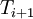 is from the previous iteration, while
is from the previous iteration, while 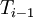 is from the current iteration:
is from the current iteration:
The following table gives the results of 10 iterations with 5 nodes (3 interior and 2 boundary) as well as 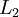 norm error.
norm error.
| Iteration | 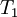 | 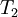 | 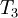 | 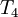 | 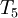 | 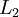 error error
|
|---|---|---|---|---|---|---|
| 0 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 1.0000E+00 | 1.0000E+00 |
| 1 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 5.0000E-01 | 1.0000E+00 | 6.1237E-01 |
| 2 | 0.0000E+00 | 0.0000E+00 | 2.5000E-01 | 6.2500E-01 | 1.0000E+00 | 3.7500E-01 |
| 3 | 0.0000E+00 | 1.2500E-01 | 3.7500E-01 | 6.8750E-01 | 1.0000E+00 | 1.8750E-01 |
| 4 | 0.0000E+00 | 1.8750E-01 | 4.3750E-01 | 7.1875E-01 | 1.0000E+00 | 9.3750E-02 |
| 5 | 0.0000E+00 | 2.1875E-01 | 4.6875E-01 | 7.3438E-01 | 1.0000E+00 | 4.6875E-02 |
| 6 | 0.0000E+00 | 2.3438E-01 | 4.8438E-01 | 7.4219E-01 | 1.0000E+00 | 2.3438E-02 |
| 7 | 0.0000E+00 | 2.4219E-01 | 4.9219E-01 | 7.4609E-01 | 1.0000E+00 | 1.1719E-02 |
| 8 | 0.0000E+00 | 2.4609E-01 | 4.9609E-01 | 7.4805E-01 | 1.0000E+00 | 5.8594E-03 |
| 9 | 0.0000E+00 | 2.4805E-01 | 4.9805E-01 | 7.4902E-01 | 1.0000E+00 | 2.9297E-03 |
| 10 | 0.0000E+00 | 2.4902E-01 | 4.9902E-01 | 7.4951E-01 | 1.0000E+00 | 1.4648E-03 |
In this situation, the direction that we "sweep" is important - if we step though the solution vector in the opposite direction, the solution moves away from the chosen initial condition (zero everywhere in the interior) more quickly. The iteration is defined by
and this gives us (slightly) faster convergence, as shown in the table below.
| Iteration | 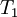 | 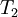 | 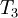 | 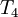 | 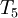 | 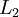 error error
|
|---|---|---|---|---|---|---|
| 0 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 1.0000E+00 | 1.0000E+00 |
| 1 | 0.0000E+00 | 1.2500E-01 | 2.5000E-01 | 5.0000E-01 | 1.0000E+00 | 3.7500E-01 |
| 2 | 0.0000E+00 | 1.8750E-01 | 3.7500E-01 | 6.2500E-01 | 1.0000E+00 | 1.8750E-01 |
| 3 | 0.0000E+00 | 2.1875E-01 | 4.3750E-01 | 6.8750E-01 | 1.0000E+00 | 9.3750E-02 |
| 4 | 0.0000E+00 | 2.3438E-01 | 4.6875E-01 | 7.1875E-01 | 1.0000E+00 | 4.6875E-02 |
| 5 | 0.0000E+00 | 2.4219E-01 | 4.8438E-01 | 7.3438E-01 | 1.0000E+00 | 2.3438E-02 |
| 6 | 0.0000E+00 | 2.4609E-01 | 4.9219E-01 | 7.4219E-01 | 1.0000E+00 | 1.1719E-02 |
| 7 | 0.0000E+00 | 2.4805E-01 | 4.9609E-01 | 7.4609E-01 | 1.0000E+00 | 5.8594E-03 |
| 8 | 0.0000E+00 | 2.4902E-01 | 4.9805E-01 | 7.4805E-01 | 1.0000E+00 | 2.9297E-03 |
| 9 | 0.0000E+00 | 2.4951E-01 | 4.9902E-01 | 7.4902E-01 | 1.0000E+00 | 1.4648E-03 |
| 10 | 0.0000E+00 | 2.4976E-01 | 4.9951E-01 | 7.4951E-01 | 1.0000E+00 | 7.3242E-04 |
For this toy example, there is not large penalty for choosing the wrong sweep direction. For some of the more complicated variants of Gauss-Seidel, there is a substantial penalty - the sweep direction determines (in a vague sense) the direction in which information travels.

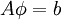
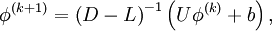
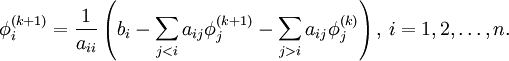
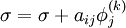
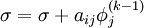
![\nabla^2 T(x) = 0,\ x\in [0,1]](/W/images/math/6/8/1/681af3c6083368314f689c744b5b198c.png)
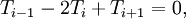
![\left[
\begin{matrix}
{1 } & {0 } & {0 } & \cdot & \cdot & { 0 } \\
{1 } & {-2 } & {1 } & { } & { } & \cdot \\
{ 0 } & {1 } & {-2 } & { 1 } & { } & \cdot \\
{ } & { } & \cdot & \cdot & \cdot & \cdot \\
{ } & { } & { } & {1 } & {-2 } & {1 }\\
{ 0 } & \cdot & \cdot & { 0 } & { 0 } & {1 }\\
\end{matrix}
\right]
\left[
\begin{matrix}
{T_1 } \\
{T_2 } \\
{T_3 } \\
\cdot \\
{T_{n-1} } \\
{T_n } \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
{0} \\
{0} \\
{0} \\
\cdot \\
{0} \\
{1} \\
\end{matrix}
\right].](/W/images/math/0/9/6/0969684693ca0c618b2b9ba12bd8695d.png)