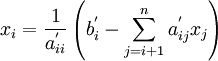Gaussian elimination
From CFD-Wiki
(Difference between revisions)
| Line 28: | Line 28: | ||
\right] | \right] | ||
</math> | </math> | ||
| + | To perform Gaussian elimination starting with the above given system of equations we compose the '''augmented matrix equation''' in the form: <br> | ||
| + | |||
| + | :<math> | ||
| + | \left[ | ||
| + | \begin{matrix} | ||
| + | {a_{11} } & {a_{12} } & {...} & {a_{1n} } \\ | ||
| + | {a_{21} } & {a_{22} } & . & {a_{21} } \\ | ||
| + | . & . & . & . \\ | ||
| + | {a_{n1} } & {a_{n1} } & . & {a_{nn} } \\ | ||
| + | \end{matrix} | ||
| + | |||
| + | \left| | ||
| + | \begin{matrix} | ||
| + | {b_1 } \\ | ||
| + | {b_2 } \\ | ||
| + | . \\ | ||
| + | {b_n } \\ | ||
| + | \end{matrix} | ||
| + | |||
| + | \right. | ||
| + | |||
| + | \right] | ||
| + | \left[ | ||
| + | \begin{matrix} | ||
| + | {x_1 } \\ | ||
| + | {x_2 } \\ | ||
| + | . \\ | ||
| + | {x_n } \\ | ||
| + | \end{matrix} | ||
| + | \right] | ||
| + | </math> <br> | ||
| + | |||
| + | After performing elementary raw operations the '''augmented matrix''' is put into the upper triangular form: <br> | ||
| + | |||
| + | :<math> | ||
| + | \left[ | ||
| + | \begin{matrix} | ||
| + | {a_{11}^' } & {a_{12}^' } & {...} & {a_{1n}^' } \\ | ||
| + | 0 & {a_{22}^' } & . & {a_{2n}^' } \\ | ||
| + | . & . & . & . \\ | ||
| + | 0 & 0 & . & {a_{nn}^' } \\ | ||
| + | \end{matrix} | ||
| + | |||
| + | \left| | ||
| + | \begin{matrix} | ||
| + | {b_1^' } \\ | ||
| + | {b_1^' } \\ | ||
| + | . \\ | ||
| + | {b_1^' } \\ | ||
| + | |||
| + | \end{matrix} | ||
| + | |||
| + | \right. | ||
| + | \right] | ||
| + | </math> <br> | ||
| + | |||
| + | By using the formula: <br> | ||
| + | :<math> | ||
| + | x_i = {1 \over {a_{ii}^' }}\left( {b_i^' - \sum\limits_{j = i + 1}^n {a_{ij}^' x_j } } \right) | ||
| + | </math> <br> | ||
| + | Solve the equation of the k<sup>th</sup> row for x<sup>k</sup>, then substitute back into the equation of the (k-1)<sup>st</sup> row to obtain a solution for (k-1)<sup>st</sup> raw, and so on till k = 1. | ||
Revision as of 07:55, 27 September 2005
Gauss Elimination
We consider the system of linear equations 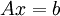 or
or
To perform Gaussian elimination starting with the above given system of equations we compose the augmented matrix equation in the form:
After performing elementary raw operations the augmented matrix is put into the upper triangular form:
By using the formula:
Solve the equation of the kth row for xk, then substitute back into the equation of the (k-1)st row to obtain a solution for (k-1)st raw, and so on till k = 1.

![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\right]
\left[
\begin{matrix}
{x_1 } \\
{x_2 } \\
. \\
{x_n } \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right]](/W/images/math/6/7/7/677a1968347218633c4702a422ca4c2a.png)
![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\left|
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right.
\right]
\left[
\begin{matrix}
{x_1 } \\
{x_2 } \\
. \\
{x_n } \\
\end{matrix}
\right]](/W/images/math/3/b/1/3b171f419df579fc32d4184f498753fa.png)
![\left[
\begin{matrix}
{a_{11}^' } & {a_{12}^' } & {...} & {a_{1n}^' } \\
0 & {a_{22}^' } & . & {a_{2n}^' } \\
. & . & . & . \\
0 & 0 & . & {a_{nn}^' } \\
\end{matrix}
\left|
\begin{matrix}
{b_1^' } \\
{b_1^' } \\
. \\
{b_1^' } \\
\end{matrix}
\right.
\right]](/W/images/math/c/f/9/cf9d0e176e3916d1cb1a925ca3b34e00.png)