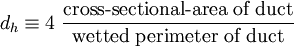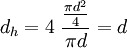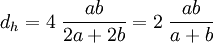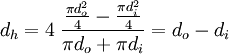Hydraulic diameter
From CFD-Wiki
m (Reverted edits by NorolRelor (Talk) to last version by Jola) |
|||
| (9 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
:<math>d_h \equiv 4 \; \frac{\mbox{cross-sectional-area of duct}}{\mbox{wetted perimeter of duct}}</math> | :<math>d_h \equiv 4 \; \frac{\mbox{cross-sectional-area of duct}}{\mbox{wetted perimeter of duct}}</math> | ||
| - | ==Circular pipe== | + | ==Use of hydraulic diameter== |
| + | |||
| + | ===Estimating the turbulent length-scale=== | ||
| + | |||
| + | For fully-developed flow in non-circular ducts the [[turbulent length scale]] can be estimated as <math>0.07 \, d_h</math>. This is as usefull estimation for setting [[turbulence boundary conditions]] for inlets that have fully developed flow. | ||
| + | |||
| + | ===Computing Reynolds number=== | ||
| + | |||
| + | The hydraulic diamater is often used when computing the dimensionless [[Reynolds number]] for non-circular ducts. | ||
| + | |||
| + | ==Hydraulic diameters for different duct-geometries== | ||
| + | |||
| + | Using the definition above the hydraulic diamater can easily be computed for any type of duct-geometry. Below follows a few examples. | ||
| + | |||
| + | ===Circular pipe=== | ||
For a circular pipe or hole the hydraulic diamater is: | For a circular pipe or hole the hydraulic diamater is: | ||
| Line 13: | Line 27: | ||
Where d is the real diameter of the pipe. Hence, for circular pipes the hydraulic diameter is the same as the real diameter of the pipe. | Where d is the real diameter of the pipe. Hence, for circular pipes the hydraulic diameter is the same as the real diameter of the pipe. | ||
| - | ==Rectangular tube== | + | ===Rectangular tube=== |
For a rectangular tube or hole with the width <math>a</math> and the height <math>b</math> the hydraulic diamter is: | For a rectangular tube or hole with the width <math>a</math> and the height <math>b</math> the hydraulic diamter is: | ||
| Line 19: | Line 33: | ||
:<math>d_h = 4 \; \frac{a b}{2 a + 2 b} = 2 \; \frac{a b}{a + b}</math> | :<math>d_h = 4 \; \frac{a b}{2 a + 2 b} = 2 \; \frac{a b}{a + b}</math> | ||
| - | ==Coaxial circular tube== | + | ===Coaxial circular tube=== |
| - | For a coaxial circular tube with an inner diameter | + | For a coaxial circular tube with an inner diameter <math>d_i</math> and an outer diameter <math>d_o</math> the hydraulic diameter is: |
:<math>d_h = 4 \; \frac{\frac{\pi d_o^2}{4} - \frac{\pi d_i^2}{4}}{\pi d_o + \pi d_i} = d_o - d_i</math> | :<math>d_h = 4 \; \frac{\frac{\pi d_o^2}{4} - \frac{\pi d_i^2}{4}}{\pi d_o + \pi d_i} = d_o - d_i</math> | ||
Latest revision as of 09:58, 17 December 2008
The hydraulic diameter,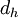 
, is commonly used when dealing with non-circular pipes, holes or ducts.
The definition of the hydraulic diamater is:
Contents |
Use of hydraulic diameter
Estimating the turbulent length-scale
For fully-developed flow in non-circular ducts the turbulent length scale can be estimated as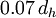 
. This is as usefull estimation for setting turbulence boundary conditions for inlets that have fully developed flow.
Computing Reynolds number
The hydraulic diamater is often used when computing the dimensionless Reynolds number for non-circular ducts.
Hydraulic diameters for different duct-geometries
Using the definition above the hydraulic diamater can easily be computed for any type of duct-geometry. Below follows a few examples.
Circular pipe
For a circular pipe or hole the hydraulic diamater is:
Where d is the real diameter of the pipe. Hence, for circular pipes the hydraulic diameter is the same as the real diameter of the pipe.
Rectangular tube
For a rectangular tube or hole with the width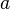 
and the height 
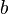the hydraulic diamter is:
Coaxial circular tube
For a coaxial circular tube with an inner diameter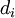 
and an outer diameter 
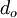the hydraulic diameter is:
