Hydrodynamic/acoustic splitting
From CFD-Wiki
| Line 21: | Line 21: | ||
<math>\frac{{\partial p'}}{{\partial t}}\!+\!(\vec u \cdot \nabla )p'\!+\!\gamma p(\nabla \cdot \vec u') + (\vec | <math>\frac{{\partial p'}}{{\partial t}}\!+\!(\vec u \cdot \nabla )p'\!+\!\gamma p(\nabla \cdot \vec u') + (\vec | ||
u' \cdot \nabla )P = - \frac{{DP}}{{Dt}} + (\gamma - 1)\left( {\Phi - \nabla \cdot \vec q} \right)</math> | u' \cdot \nabla )P = - \frac{{DP}}{{Dt}} + (\gamma - 1)\left( {\Phi - \nabla \cdot \vec q} \right)</math> | ||
| + | |||
| + | where <math>D/Dt = \partial /\partial t + (\vec U \cdot \nabla )</math>, <math>\vec f'_{vis}</math> is the perturbed viscous force | ||
| + | vector, <math>\Phi</math> and <math>\vec q</math> represent thermal viscous dissipation and heat flux vector, respectively. | ||
| + | The PCE are the mixed-scales, non-linear equations, in which terms are involved with coupling effects between the acoustic | ||
| + | fluctuations and the incompressible flow field. Through the coupling effects, a non-radiating vortical component, so-called | ||
| + | 'perturbed vorticity', is generated in the perturbed system. The perturbed vorticity may be regarded as the modification of | ||
| + | hydrodynamic vorticity due to acoustic fluctuations, but it just reside in the perturbed system by this 'one-way' splitting method, | ||
| + | in which backscattering of acoustic fluctuations onto the incompressible flow field is prohibited. | ||
Revision as of 21:35, 30 July 2008
In the hydrodynamic/acoustic splitting method, the total flow variables are decomposed into the incompressible variables and the perturbed compressible ones as,
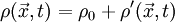
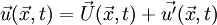
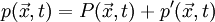
The incompressible variables represent the hydrodynamic flow field, while the acoustic fluctuations and other compressibility effects are resolved by the perturbed quantities denoted by ('). The original full perturbed compressible equations (PCE) to calculate the perturbed quantities can be derived by subtracting the incompressible Navier-Stokes equations from the compressible ones. The PCE recently revised by Seo and Moon are written in a vector form as,
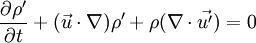
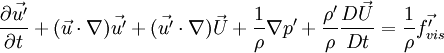
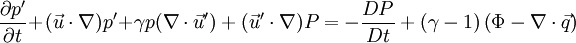
where 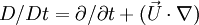 ,
, 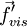 is the perturbed viscous force
vector,
is the perturbed viscous force
vector, 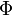 and
and 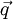 represent thermal viscous dissipation and heat flux vector, respectively.
The PCE are the mixed-scales, non-linear equations, in which terms are involved with coupling effects between the acoustic
fluctuations and the incompressible flow field. Through the coupling effects, a non-radiating vortical component, so-called
'perturbed vorticity', is generated in the perturbed system. The perturbed vorticity may be regarded as the modification of
hydrodynamic vorticity due to acoustic fluctuations, but it just reside in the perturbed system by this 'one-way' splitting method,
in which backscattering of acoustic fluctuations onto the incompressible flow field is prohibited.
represent thermal viscous dissipation and heat flux vector, respectively.
The PCE are the mixed-scales, non-linear equations, in which terms are involved with coupling effects between the acoustic
fluctuations and the incompressible flow field. Through the coupling effects, a non-radiating vortical component, so-called
'perturbed vorticity', is generated in the perturbed system. The perturbed vorticity may be regarded as the modification of
hydrodynamic vorticity due to acoustic fluctuations, but it just reside in the perturbed system by this 'one-way' splitting method,
in which backscattering of acoustic fluctuations onto the incompressible flow field is prohibited.
